
【题目】已知直线![]() 恒过定点
恒过定点![]() ,圆
,圆![]() 经过点
经过点![]() 和定点
和定点![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)已知点![]() 为圆
为圆![]() 直径的一个端点,若另一端点为点
直径的一个端点,若另一端点为点![]() ,问
,问![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为直角三角形,若存在,求出
为直角三角形,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)从某厂生产的一批零件1000个中抽取20个进行研究,应采用什么抽样方法?
(2)对(1)中的20个零件的直径进行测量,得到下列不完整的频率分布表:(单位:mm)
分组 | 频数 | 频率 |
| 2 | |
| 6 | |
| 8 | |
| ||
合计 | 20 | 1 |
①完成频率分布表;
②画出其频率分布直方图.
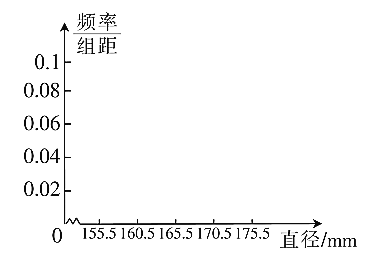
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过直线2x+y-5=0与x-2y=0的交点P.
(1)若直线l平行于直线l1:4x-y+1=0,求l的方程;
(2)若直线l垂直于直线l1:4x-y+1=0,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将各项均为整数的数列![]() 排成如图所示的三角形数阵(第
排成如图所示的三角形数阵(第![]() 行有
行有![]() 个数,同一行中,下标小的数排在左边).
个数,同一行中,下标小的数排在左边).![]() 表示数阵中第
表示数阵中第![]() 行第1列的数.
行第1列的数.
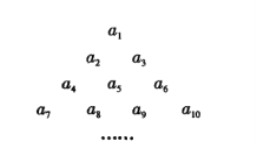
已知数列![]() 为等比数列,且从第3行开始,各行均构成公差为
为等比数列,且从第3行开始,各行均构成公差为![]() 的等差数列,
的等差数列,![]() ,
,![]() ,
,![]() .
.
(1)求数阵中第![]() 行 第
行 第![]() 列的数
列的数 ![]() (用
(用 ![]() 、
、![]() 表示);
表示);
(2)求![]() 的值;
的值;
(3)2013是否在该数阵中,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 y = x3 + x-2 在点 P0 处的切线![]() 平行于直线
平行于直线
4x-y-1=0,且点 P0 在第三象限,
⑴求P0的坐标;
⑵若直线![]() , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科赫曲线是一种外形像雪花的几何曲线,一段科赫曲线可以通过下列操作步骤构造得到,任画一条线段,然后把它均分成三等分,以中间一段为边向外作正三角形,并把中间一段去掉,这样,原来的一条线段就变成了4条小线段构成的折线,称为“一次构造”;用同样的方法把每条小线段重复上述步骤,得到16条更小的线段构成的折线,称为“二次构造”,…,如此进行“![]() 次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取
次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取![]() ,
,![]() )
)

A.16B.17C.24D.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》里有一道关于玉石的问题:“今有玉方一寸,重七两;石方一寸,重六两.今有石方三寸,中有玉,并重十一斤(176两)问玉、石重各几何?”如图所示的程序框图反映了对此题的一个求解算法,运行该程序框图,则输出的![]() ,
,![]() 分别为( )
分别为( )

A.98,78B.96,80C.94,74D.92,72
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com