
����Ŀ������ʱ��3��15�����磬�ȸ�Χ���˹����� ![]() �뺫����������ʯ�������һ�ֽ�����
�뺫����������ʯ�������һ�ֽ����� ![]() ��ñ�������ʤ���������˻���ս�ܱȷֶ���
��ñ�������ʤ���������˻���ս�ܱȷֶ��� ![]() .�˻���սҲ����ȫ���Χ��Ĺ�ע��ijѧУ����Ϊ����ѧ��ѧϰΧ�������������ȡ��100��ѧ�����е���.���ݵ��������Ƶ�ѧ���վ�ѧϰΧ��ʱ���Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�������վ�ѧϰΧ��ʱ�䲻����40���ӵ�ѧ����Ϊ��Χ���ԡ�.
.�˻���սҲ����ȫ���Χ��Ĺ�ע��ijѧУ����Ϊ����ѧ��ѧϰΧ�������������ȡ��100��ѧ�����е���.���ݵ��������Ƶ�ѧ���վ�ѧϰΧ��ʱ���Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�������վ�ѧϰΧ��ʱ�䲻����40���ӵ�ѧ����Ϊ��Χ���ԡ�.
��������֪�����������������������ݴ��������Ƿ��� ![]() �İ�����Ϊ��Χ���ԡ����Ա��йأ�
�İ�����Ϊ��Χ���ԡ����Ա��йأ�
��Χ���� | Χ���� | �ϼ� | |
�� | |||
Ů | 10 | 55 | |
�ϼ� |
���������������õ���Ƶ����Ϊ���ʣ����ڴӸõ�������ѧ���У����������������ÿ�γ�ȡ1��ѧ������ȡ3�Σ��DZ���ȡ��3���������еġ�Χ���ԡ�����Ϊ ![]() ����ÿ�γ�ȡ�Ľ����������ģ���
����ÿ�γ�ȡ�Ľ����������ģ��� ![]() �ķֲ��У�����
�ķֲ��У����� ![]() �ͷ���
�ͷ��� ![]() .
.
���� ![]() ������
������ ![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
���𰸡��⣺������Ƶ�ʷֲ�ֱ��ͼ��֪���ڳ�ȡ��100���У���Χ���ԡ���25�ˣ��Ӷ� ![]() ����������
����������
��Χ���� | Χ���� | �ϼ� | |
�� | 30 | 15 | 45 |
Ů | 45 | 10 | 55 |
�ϼ� | 75 | 25 | 100 |
�� ![]() �������е����ݴ��빫ʽ���㣬��
�������е����ݴ��빫ʽ���㣬��![]()
��Ϊ ![]() ������û��������Ϊ��Χ���ԡ����Ա��й�.
������û��������Ϊ��Χ���ԡ����Ա��й�.
������Ƶ�ʷֲ�ֱ��ͼ֪�鵽��Χ���ԡ���Ƶ��Ϊ0.25����Ƶ����Ϊ���ʣ����ӹ����г�ȡһ����Χ���ԡ��ĸ���Ϊ ![]() .������
.������ ![]() ���Ӷ�
���Ӷ� ![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
. ![]() .
.
��������������Ҫ������Ƶ�ʷֲ�ֱ��ͼ���Լ�����������ѧ��������Ӧ�á���1������Ƶ�ʷֲ�ֱ��ͼ��д2��2�ֲ�ͼ������۲�ֵ���Ƚ��ٽ�ֵ���ɵý��ۡ���2����Ƶ�ʷֲ�ֱ��ͼ����Ƶ�ʣ���Ƶ����Ϊ���ʣ�Ȼ���ɷֲ��У�������ѧ����������⡣
�����㾫�����������⣬������Ҫ�˽�Ƶ�ʷֲ�ֱ��ͼ(Ƶ�ʷֲ������ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ)��


 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��
��
��1��֤����k��R��ֱ��y=g��x������������y=f��x�������ߣ�
��2����x��[e��e2]��ʹ��f��x����g��x��+ ![]() ��������ʵ��k��ȡֵ��Χ��
��������ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() ��������Ϊ
��������Ϊ ![]() ����ΪF����1��0��������D��0��2����б��Ϊk��ֱ��l����Բ��A��B���㣮
����ΪF����1��0��������D��0��2����б��Ϊk��ֱ��l����Բ��A��B���㣮
��1������ԲC�ı����̣�
��2����y���ϣ��Ƿ���ڶ���E��ʹ ![]() ��Ϊ��ֵ�������ڣ����E�������������ֵ���������ڣ�˵�����ɣ�
��Ϊ��ֵ�������ڣ����E�������������ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABC�У���ABC���������Σ���ACP��ֱ�������Σ���ABP=��CBP��AB=BP��
��1��֤����ƽ��ACP��ƽ��ABC��
��2����EΪ��PB��P���غϵĵ㣬��AE��CE����AE��ƽ��ABC���ɵĽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ax2��bx��c��0�Ľ⼯Ϊ{x|x����2����x��4}������ں���f(x)��ax2��bx��cӦ��( )
A.f(5)��f(2)��f(��1)
B.f(5)��f(��1)��f(2)
C.f(��1)��f(2)��f(5)
D.f(2)��f(��1)��f(5)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ν��������ָ���ǵ���Ϊ�������Σ������ڵ����ϵ���ӰΪ�������������ĵ��������������� ![]() �У�
�� ![]() ��
�� ![]() ���е㣬��
���е㣬�� ![]() ������߳�
������߳� ![]() ����������
���������� ![]() �����Ϊ �� �������ı����Ϊ ��
�����Ϊ �� �������ı����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ĸ����⣺
p1��x0��(0������)�� ![]() <
< ![]() ��
��
p2��x0�� ![]() ��
�� ![]() ��
�� ![]() ��
��
p3��x��R,2x>x2��
p4��x��(1������)�� ![]()
������������( )
A.p1 �� p3
B.p1 �� p4
C.p2 �� p3
D.p2 �� p4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������� ![]() �У�
�У� ![]() ,ƽ��
,ƽ�� ![]()
![]() ƽ��
ƽ�� ![]() ��
�� ![]() ��
�� ![]() �ֱ�Ϊ
�ֱ�Ϊ ![]() ��
�� ![]() ���е㣮
���е㣮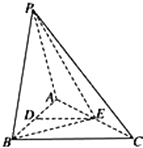
��1����֤�� ![]()
![]() ƽ��
ƽ�� ![]() ��
��
��2����֤�� ![]() ��
��
��3�������� ![]() �������
�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com