
分析 (1)确定二次函数的图象关键因素(开口方向、对称轴、顶点坐标),由图象可直接写出单调区间;
(2)根据对称轴与给定区间的位置关系分三种情况讨论,得到函数的最小值.
解答 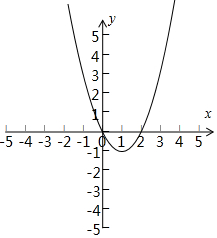 解:(1)图象如图:
解:(1)图象如图:
减区间为:(-∞,1];
证明:设x1<x2≤1,
则f(x1)-f(x2)=x12-2x1-(${{x}_{2}}^{2}$-2x2)
=(x1-x2)(x1+x2)-2(x1-x2)
=(x1-x2)(x1+x2-2)
∵x1<x2≤1,
∴x1-x2<0,x1+x2-2<0,
∴(x1-x2)(x1+x2-2)>0,
∴f(x1)>f(x2).
∴函数f(x)单调减区间为(-∞,1].
(2)①当a+1≤1即a≤0时,[a,a+1]⊆(-∞,1],则f(x)在[a,a+1]上是减函数,
∴当x=a+1时,函数f(x)=x2-2x的最小值f(a+1)=a2-1.
同理,②当0<a≤1时,函数f(x)=x2-2x的最小值f(1)=-1.
③当a>1时,函数f(x)=x2-2x的最小值f(a)=a2-2a.
点评 本题考查二次函数的简单性质的应用,考查分类讨论思想的应用,数形结合思想的应用,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 5 | C. | 7 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=3,BC=7$\sqrt{3}$,CD=14,BD=7,∠BAD=120°.
如图,在四边形ABCD中,AB=3,BC=7$\sqrt{3}$,CD=14,BD=7,∠BAD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,3) | B. | {4,-3} | C. | {(4,3)} | D. | {(4,-3)} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 技术改造的月份x | 1 | 2 | 3 | 4 |
| 煤炭消耗量y | 4.5 | 4 | 3 | 2.5 |
| A. | $\widehat{y}$=0.7x+5.25 | B. | $\widehat{y}$=-0.6x+5.25 | C. | $\widehat{y}$=-0.7x+6.25 | D. | $\widehat{y}$=-0.7x+5.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com