练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在下列命题中，假命题是（　　）
    A、存在x∈R，lgx=0
    B、存在x∈R，tanx=0
    C、任意x∈R，2x＞0
    D、任意x∈R，x3＞0
    考点：命题的真假判断与应用
    专题：简易逻辑
    分析：A．取x=1，使得lgx=0；
    B．取x=0，则tan0=0；
    C．?x∈R，2x＞0；
    D．取x=-1，（-1）3＜0，即可判断出．
    解答： 解：对于A．取x=1，使得lgx=0，正确；
    对于B．取x=0，则tan0=0，正确；
    对于C．?x∈R，2x＞0，正确；
    对于D．取x=-1，（-1）3＜0，因此不正确．
    故选：D．
    点评：本题考查了简易逻辑的判定、举反例否定一个命题的方法，考查了推理能力，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

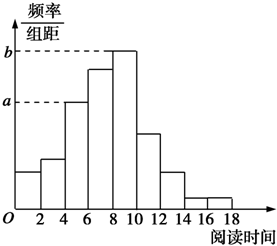    从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频率分布表和频率分布直方图：
    分组频数频率
    [0，2）60.06
    [2，4）80.08
    [4，6）170.17
    [6，8）200.20
    [8，10）
    [10，12）140.14
    [12，14）6
    [14，16）20.02
    [16，18）0.02
      合计1001.00
    （Ⅰ）补全频率分布表，并求频率分布直方图中的a，b．
    （Ⅱ）若该校有2000人，现需调查长时间阅读对视力的影响程度，阅读时间不低于14小时的学生应抽取多少人？
    （Ⅲ）试估计样本的100名学生该周阅读时间的中位数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在等腰梯形ABCD中，对角线AC⊥BD，且相交于点O，E是AB边的中点，EO的延长线交CD于F．
    （1）求证：EF⊥CD；
    （2）若∠ABD=30°，求证S△ODF：S△ODC=1：4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    有下列四个命题：
    ①“若a2+b2=0，则a，b全为0”的逆否命题；
    ②“全等三角形的面积相等”的否命题；
    ③“若“q≤1”，则x2+2x+q=0有实根”的逆否命题；
    ④“矩形的对角线相等”的逆命题．
    其中真命题为（　　）
    A、①②B、①③C、②③D、③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若
    a
    ，
    b
    均为单位向量，且
    a
    •
    b
    =0，（
    a
    -
    c
    ）•（
    b
    -
    c
    ）≤0，则|2
    a
    -
    c
    |的最大值为（　　）
    A、
    		10
    +
    		2
    2
    B、
    		10
    -
    		2
    2
    C、
    		2
    D、
    		2
    +2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知z∈C，
    .
    z
    为z的共轭复数，若
    .
    ziz
    1
    .
    z
    .
    =0（z≠0）（i是虚数单位），则z=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列运算正确的是（　　）
    A、（ax2-bx+c）′=a（x2）′+b（-x）′
    B、（cosx•sinx）′=（sinx）′•cosx+（cosx）′•cosx
    C、（sinx-2x2）′=（sinx）′-（2）′（x2）′
    D、[（3+x2）（2-x3）]′=2x（2-x3）+3x2（3+x2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=loga（x+1）是定义在区间[1，7]上的函数，且最大值与最小值之和是2，求函数f（x）的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    化简
    sinα+sinβ
    cosα+cosβ
    为
     
    ．

    查看答案和解析>>

    同步练习册答案