

|
| 25+y2 |
| 119 |
| 24 |
| 119 |
| 24 |
|
| 25+y2 |
| 119 |
| 24 |
|
| 25+y2 |
| 119 |
| 24 |
| 119 |
| 24 |
|
| 119 |
| 24 |
| AC2-OC2 |
| π |
| 4 |
| 119 |
| 24 |
| 119 |
| 24 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
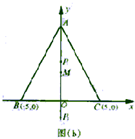
 (2003•北京)有三个新兴城镇,分别位于A,B,C三点处,且AB=AC=13km,BC=10km.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处,(建立坐标系如图)
(2003•北京)有三个新兴城镇,分别位于A,B,C三点处,且AB=AC=13km,BC=10km.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处,(建立坐标系如图)查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012年人教B版高中数学必修5 3.4 不等式的实际应用练习卷(解析版) 题型:解答题
有三个新兴城镇,分别位于A、B、C三个点处,且AB=AC=13千米,BC=10千米。今计划合建一个中心医院。为同时方便三个城镇,需要将医院建在BC的垂直平分线上的点P处。若希望点P到三个城镇距离的平方和最小,点P应该位于何处?
查看答案和解析>>
科目:高中数学 来源:北京高考真题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com