
 如图,△ABC中的阴影部分是由曲线y=x2与直线x-y+2=0所围成,向△ABC内随机投掷一点,则该点落在阴影部分的概率为$\frac{9}{16}$.
如图,△ABC中的阴影部分是由曲线y=x2与直线x-y+2=0所围成,向△ABC内随机投掷一点,则该点落在阴影部分的概率为$\frac{9}{16}$. 分析 由题意,本题是几何概型,首先求出三角形面积,以及利用定积分求出阴影部分的面积,然后由几何概型的公式求概率.
解答 解:由已知△ABC的面积为$\frac{1}{2}×4×4$=8,阴影部分面积为
$\int_{-1}^2{(x+2-{x^2}})dx=(\frac{x^2}{2}+2x-\frac{x^3}{3})\left|{\begin{array}{l}2\\{-1}\end{array}}\right.=\frac{9}{2}$,
由几何概型的公式得到所求概率为$\frac{{\frac{9}{2}}}{{\frac{1}{2}×4×4}}=\frac{9}{16}$;
故答案为:$\frac{9}{16}$.
点评 本题考查了定积分的运用以及几何概型的概率求法;正确求出阴影部分面积,利用面积比求概率.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
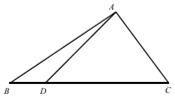 如图,在△ABC中,点D在BC边上,α=∠BAD,(1+tanα)(1+tanβ)=2,cosC=$\frac{3}{5}$.
如图,在△ABC中,点D在BC边上,α=∠BAD,(1+tanα)(1+tanβ)=2,cosC=$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | b>c>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com