
【题目】已知![]() 为自然对数的底数,
为自然对数的底数, ![]() ).
).
(1)设![]() 为
为![]() 的导函数,证明:当
的导函数,证明:当![]() 时,
时, ![]() 的最小值小于0;
的最小值小于0;
(2)若![]() 恒成立,求符合条件的最小整数
恒成立,求符合条件的最小整数![]()
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)先对函数进行求导,然后再对导函数进行求导,判断导函数的单调性与单调区间,利用单调性确定到导函数的最小值;(2)先根据条件,确定问题即求函数的最小值大于0,然后对函数进行求导,利用函数的单调性及零点存在定理确定函数存在零点,并表示零点,然后通过不等式恒成立,确定关于![]() 的关系式,再对该关系式进行求导,利用导数判断单调性,求得
的关系式,再对该关系式进行求导,利用导数判断单调性,求得![]() 的取值范围,最后得到其取到的最小整数.
的取值范围,最后得到其取到的最小整数.
试题解析:(1)令![]() ,则
,则![]()
因为![]() ,令
,令![]() ,则
,则![]() .
.
所以当![]() 时,
时, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() 单调递增.
单调递增.
则![]() =
= ![]() =
= ![]() =
=![]() =
=![]()
令![]() ,
,![]()
当![]() 时,
时, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() 单调递减.
单调递减.
所以![]() ,所以
,所以![]() 成立.
成立.
(2) ![]() 恒成立,等价于
恒成立,等价于![]() 恒成立.
恒成立.
令![]() ,
,
则![]() 因为
因为![]() ,所以
,所以![]() ,所以
,所以![]() 单调递增.
单调递增.
又![]() ,
,
所以存在![]() ,使得
,使得![]() .
.
则![]() 时,
时, ![]() 单调递减;
单调递减;
![]() 时,
时, ![]() 单调递增.
单调递增.
所以![]() 恒成立. ①
恒成立. ①
且![]() ②
②
由①②得![]() =
= =
=![]() 恒成立.
恒成立.
又由②得![]() ,
,
所以![]()
![]() ,
,
所以![]() ,
,
所以![]() 单调递增,
单调递增, ![]() =
=![]() ,
,
![]() =
=![]() ,
,
所以![]() ,所以符合条件的最小整数
,所以符合条件的最小整数![]() .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1的中点,且FD⊥AC1,有下述结论:
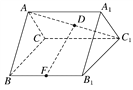
①AC1⊥BC;
②![]() =1;
=1;
③平面FAC1⊥平面ACC1A1;
④三棱锥D-ACF的体积为![]() .
.
其中正确结论的个数为( )
A. 1 B. 2
C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ln(x-1),其中a为常数.
(1)试讨论f(x)的单调区间;
(2)当a=![]() 时,存在x使得不等式
时,存在x使得不等式![]() 成立,求b的取值范围.
成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题12分)如图,在海岸线![]() 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段
一侧有一休闲游乐场,游乐场的前一部分边界为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
,![]() 的图像,图像的最高点为
的图像,图像的最高点为![]() .边界的中间部分为长
.边界的中间部分为长![]() 千米的直线段
千米的直线段![]() ,且
,且![]() .游乐场的后一部分边界是以
.游乐场的后一部分边界是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.

(1)求曲线段![]() 的函数表达式;
的函数表达式;
(2)曲线段![]() 上的入口
上的入口![]() 距海岸线
距海岸线![]() 最近距离为
最近距离为![]() 千米,现准备从入口
千米,现准备从入口![]() 修一条笔直的景观路到
修一条笔直的景观路到![]() ,求景观路
,求景观路![]() 长;
长;
(3)如图,在扇形![]() 区域内建一个平行四边形休闲区
区域内建一个平行四边形休闲区![]() ,平行四边形的一边在海岸线
,平行四边形的一边在海岸线![]() 上,一边在半径
上,一边在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求平行四边形休闲区
,求平行四边形休闲区![]() 面积的最大值及此时
面积的最大值及此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1以直线![]() 所过的定点为一个焦点,且短轴长为4.
所过的定点为一个焦点,且短轴长为4.
(Ⅰ)求椭圆C1的标准方程;
(Ⅱ)已知椭圆C2的中心在原点,焦点在y轴上,且长轴和短轴的长分别是椭圆C1的长轴和短轴的长的倍(>1),过点C(1,0)的直线l与椭圆C2交于A,B两个不同的点,若![]() ,求△OAB的面积取得最大值时直线l的方程.
,求△OAB的面积取得最大值时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com