
(2012•厦门模拟)本小题设有(1)(2)(3)三个选考题,每题7分,请考生任选两题作答,满分14分,如果多做,则按所做的前两题计分.
(1)选修4﹣2:矩阵与变换
已知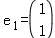 是矩阵
是矩阵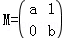 属于特征值λ1=2的一个特征向量.
属于特征值λ1=2的一个特征向量.
(I)求矩阵M;
(Ⅱ)若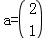 ,求M10a.
,求M10a.
(2)选修4﹣4:坐标系与参数方程
在平面直角坐标系xOy中,A(l,0),B(2,0)是两个定点,曲线C的参数方程为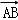 为参数).
为参数).
(I)将曲线C的参数方程化为普通方程;
(Ⅱ)以A(l,0为极点,|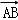 |为长度单位,射线AB为极轴建立极坐标系,求曲线C的极坐标方程.
|为长度单位,射线AB为极轴建立极坐标系,求曲线C的极坐标方程.
(3)选修4﹣5:不等式选讲
(I)试证明柯西不等式:(a2+b2)(x2+y2)≥(ax+by)2(a,b,x,y∈R);
(Ⅱ)若x2+y2=2,且|x|≠|y|,求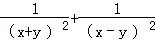 的最小值.
的最小值.
见解析
【解析】
试题分析:(1)(I)由题意,根据特征值与特征向量的定义,建立方程组,即可求得矩阵M;
(Ⅱ)求出矩阵M的特征多项式为f(λ)=(λ﹣1)(λ﹣2),从而可求矩阵M的另一个特征值与特征向量,将向量用特征向量线性表示,进而可求结论;
(2)(I)由 消去θ,即可得普通方程;
消去θ,即可得普通方程;
(Ⅱ)将原点移至A(1,0),则相应曲线C的方程为(x﹣1)2+y2=1,从而可得曲线C的极坐标方程;
(3)(I)利用作差法即可证得;
(Ⅱ)令u=x+y,v=x﹣y,则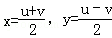 ,根据
,根据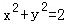 ,可得u2+v2=4,由柯西不等式得:
,可得u2+v2=4,由柯西不等式得: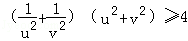 ,从而可求
,从而可求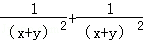 的最小值.
的最小值.
(1)【解析】
(I)由题意, ,∴
,∴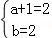 ,∴a=1,b=2
,∴a=1,b=2
∴矩阵M=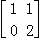 ;
;
(Ⅱ)由(I)知,矩阵M的特征多项式为f(λ)=(λ﹣1)(λ﹣2)
∴矩阵M的另一个特征值为λ2=1
设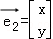 是矩阵M属于特征值1的特征向量,则
是矩阵M属于特征值1的特征向量,则
∴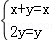 ,取x=1,则
,取x=1,则
∴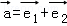
∴ =
=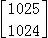
(2)(I)由 消去θ可得(x﹣2)2+y2=1;
消去θ可得(x﹣2)2+y2=1;
(Ⅱ)将原点移至A(1,0),则相应曲线C的方程为(x﹣1)2+y2=1,即x2+y2﹣2x=0
∴曲线C的极坐标方程为ρ﹣2cosθ=0
(3)(I)证明:左边﹣右边=a2y2+b2x2﹣2abxy=(ay﹣bx)2≥0,∴左边≥右边
即
(Ⅱ)令u=x+y,v=x﹣y,则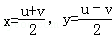
∵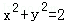 ,∴(u+v)2+(u﹣v)2=8,∴u2+v2=4
,∴(u+v)2+(u﹣v)2=8,∴u2+v2=4
由柯西不等式得: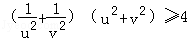 ,当且仅当
,当且仅当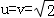 ,即
,即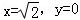 或
或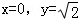 时,
时, 的最小值是1.
的最小值是1.


科目:高中数学 来源:[同步]2014年新人教A版选修4-2 3.3逆矩阵与二元一次方程组(解析版) 题型:填空题
(2014•杨浦区三模)已知一个关于x,y的二元线性方程组的增广矩阵是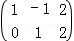 ,则x+y= .
,则x+y= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 2.1复合变换与二阶矩阵的乘法(解析版) 题型:解答题
已知矩阵A=[f(x)],B=[x 1﹣x],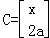 ,若A=BC,求函数f(x)在[1,2]上的最小值.
,若A=BC,求函数f(x)在[1,2]上的最小值.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.3线性变换的基本性质练习卷(解析版) 题型:选择题
(2013•黄埔区一模)若矩阵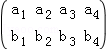 满足下列条件:①每行中的四个数所构成的集合均为{1,2,3,4};②四列中至少有两列的上下两数是相同的.则这样的不同矩阵的个数为( )
满足下列条件:①每行中的四个数所构成的集合均为{1,2,3,4};②四列中至少有两列的上下两数是相同的.则这样的不同矩阵的个数为( )
A.48 B.72 C.168 D.312
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
在同一坐标系中,将曲线y=2sin3x变为曲线y=sinx的伸缩变换是( )
A.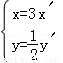 B.
B.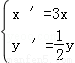
C.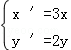 D.
D.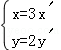
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com