
【题目】下列结论错误的是 ( )
A. 若“![]() 且
且![]() ”与“
”与“![]() 或
或![]() ”均为假命题,则
”均为假命题,则![]() 真
真![]() 假.
假.
B. 命题“存在![]() ”的否定是“对任意
”的否定是“对任意![]() ”
”
C. “![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
D. “若![]() 则a<b”的逆命题为真.
则a<b”的逆命题为真.
【答案】D
【解析】
A、对于简单命题p、q,p、q有一个假p∧q假,p、q有一个真p∨q真;
B、特称命题的否定是全称命题,全称命题的否定是特称命题;
C、pq且q推不出p,则p是q的充分不必要条件;
D、写出逆命题,由条件不能得结论,只要一个反例就可.
∵![]() 或
或![]() 为假命题,∴p和q都是假的,即p真q假,p∧q为假命题也成立,∴A正确;
为假命题,∴p和q都是假的,即p真q假,p∧q为假命题也成立,∴A正确;
∵特称命题的否定是全称命题,∴B正确;
∵x=1时,x2﹣3x+2=0成立,x2﹣3x+2=0时,x=1不一定成立,x=2也可,∴x=1是x2﹣3x+2=0”充分不必要条件,∴C正确;
逆命题为:若a<b,则am2<bm2,当m=0时,此命题不成立,∴D错误.
故选:D.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】如果直线y=kx+1与圆x2+y2+kx+my﹣4=0交于M、N两点,且M、N关于直线x+y=0对称,则不等式组: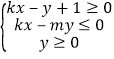 表示的平面区域的面积是( )
表示的平面区域的面积是( )
A.![]()
B.![]()
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等比数列,前n项和为Sn(n∈N*),且 ![]() ﹣
﹣ ![]() =
= ![]() ,S6=63.
,S6=63.
(1)求{an}的通项公式;
(2)若对任意的n∈N* , bn是log2an和log2an+1的等差中项,求数列{(﹣1)n bn2}的前2n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆C1的参数方程为![]() (t为参数).以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=4sinθ.
(t为参数).以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=4sinθ.
(1)写出圆C1的极坐标方程,并求圆C1与圆C2的公共弦的长度d;
(2)设射线θ=![]() 与圆C1异于极点的交点为A,与圆C2异于极点的交点为B,求|AB|.
与圆C1异于极点的交点为A,与圆C2异于极点的交点为B,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=2 ![]() sin(π﹣x)sinx﹣(sinx﹣cosx)2 .
sin(π﹣x)sinx﹣(sinx﹣cosx)2 .
(1)求f(x)的单调递增区间;
(2)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移 ![]() 个单位,得到函数y=g(x)的图象,求g(
个单位,得到函数y=g(x)的图象,求g( ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示(把频率当作概率).

(1)求甲、乙两人成绩的平均数和中位数;
(2)现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司咪推广线下分店,计划在![]() 市的
市的![]() 区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记
区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记![]() 表示在各区开设分店的个数,
表示在各区开设分店的个数, ![]() 表示这个
表示这个![]() 个分店的年收入之和.
个分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)假设该公司在![]() 区获得的总年利润
区获得的总年利润![]() (单位:百万元)与
(单位:百万元)与![]() 之间的关系为
之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在
,请结合(1)中的线性回归方程,估算该公司应在![]() 区开设多少个分店时,才能使
区开设多少个分店时,才能使![]() 区平均每个店的年利润最大?
区平均每个店的年利润最大?
(参考公式: ![]() ,其中
,其中 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com