
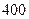 吨水,每天零点开始向居民供水,同时以每小时
吨水,每天零点开始向居民供水,同时以每小时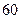 吨的速度向池中注水.已知
吨的速度向池中注水.已知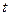 小时内向居民供水总量为
小时内向居民供水总量为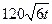 吨
吨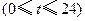 ,问
,问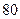 吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?
吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?科目:高中数学 来源:不详 题型:解答题
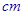 的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积
的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积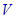 与
与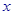 的函数关系式,并求出函数的定义域.
的函数关系式,并求出函数的定义域. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
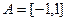 ,
,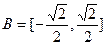 ,函数
,函数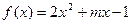 ,
,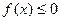 的解集为C,当
的解集为C,当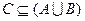 时,求实数
时,求实数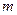 取值范围;
取值范围;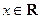 ,都有
,都有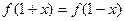 成立,试求
成立,试求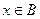 时,
时,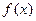 的值
的值 域;
域;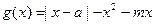
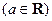 ,求
,求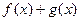 的最
的最 小值.
小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
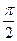 ,0)是函数y=f(x)图象的一个对称中心;
,0)是函数y=f(x)图象的一个对称中心;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com