
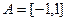 ,
,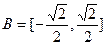 ,函数
,函数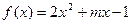 ,
,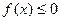 的解集为C,当
的解集为C,当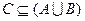 时,求实数
时,求实数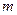 取值范围;
取值范围;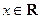 ,都有
,都有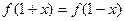 成立,试求
成立,试求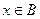 时,
时,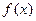 的值
的值 域;
域;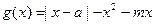
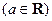 ,求
,求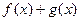 的最
的最 小值.
小值. 目标测试系列答案
目标测试系列答案科目:高中数学 来源:不详 题型:解答题
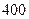 吨水,每天零点开始向居民供水,同时以每小时
吨水,每天零点开始向居民供水,同时以每小时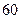 吨的速度向池中注水.已知
吨的速度向池中注水.已知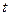 小时内向居民供水总量为
小时内向居民供水总量为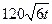 吨
吨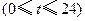 ,问
,问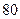 吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?
吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
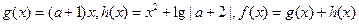 ,其中
,其中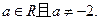
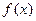 为偶函数,求a的值;
为偶函数,求a的值;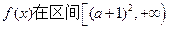 上是增函数,命题q:函数
上是增函数,命题q:函数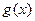 是减函数,如果p或q为真,p且q为假,求a的取值范围。
是减函数,如果p或q为真,p且q为假,求a的取值范围。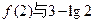 的大小。
的大小。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
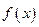 的定义域为
的定义域为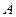 ,若
,若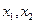
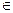
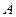 ,且
,且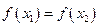
 时总有
时总有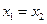 ,则称
,则称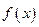 为单一函数.如
为单一函数.如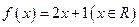 是单一函数,下列命题正确的是____▲____.(写出所有正确答案)
是单一函数,下列命题正确的是____▲____.(写出所有正确答案)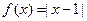
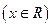 是单一函数;
是单一函数;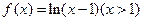 是单一函数;
是单一函数; 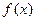 为单一函数,
为单一函数,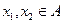 且
且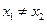 ,则
,则
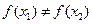 ;
; 定是单调函数.
定是单调函数. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com