
【题目】在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40 ![]() 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ= ![]() ,0°<θ<90°)且与点A相距10
,0°<θ<90°)且与点A相距10 ![]() 海里的位置C. (Ⅰ)求该船的行驶速度(单位:海里/小时);
海里的位置C. (Ⅰ)求该船的行驶速度(单位:海里/小时);
(Ⅱ)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
【答案】解:(Ⅰ)如图, 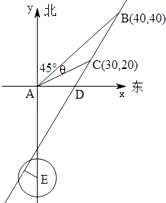
AB=40 ![]() ,AC=10
,AC=10 ![]() ,
, ![]() .
.
由于0°<θ<90°,所以cosθ= 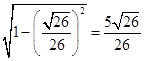 .
.
由余弦定理得BC= ![]() .
.
所以船的行驶速度为 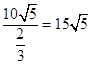 (海里/小时).
(海里/小时).
(Ⅱ)如图所示,设直线AE与BC的延长线相交于点Q.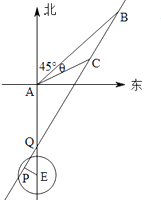
在△ABC中,由余弦定理得,![]() =
= ![]() =
= ![]() .
.
从而 ![]() .
.
在△ABQ中,由正弦定理得,
AQ= 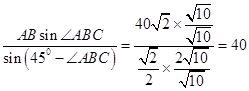 .
.
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE﹣AQ=15.
过点E作EP⊥BC于点P,则EP为点E到直线BC的距离.
在Rt△QPE中,PE=QEsin∠PQE=QEsin∠AQC=QEsin(45°﹣∠ABC)
= ![]() .
.
所以船会进入警戒水域.
【解析】(1)先根据题意画出简图确定AB、AC、∠BAC的值,根据sinθ= ![]() 求出θ的余弦值,再由余弦定理求出BC的值,从而可得到船的行驶速度.(2)先假设直线AE与BC的延长线相交于点Q,根据余弦定理求出cos∠ABC的值,进而可得到sin∠ABC的值,再由正弦定理可得AQ的长度,从而可确定Q在点A和点E之间,根据QE=AE﹣AQ求出QE的长度,然后过点E作EP⊥BC于点P,则EP为点E到直线BC的距离,进而在Rt△QPE中求出PE的值在于7进行比较即可得到答案.
求出θ的余弦值,再由余弦定理求出BC的值,从而可得到船的行驶速度.(2)先假设直线AE与BC的延长线相交于点Q,根据余弦定理求出cos∠ABC的值,进而可得到sin∠ABC的值,再由正弦定理可得AQ的长度,从而可确定Q在点A和点E之间,根据QE=AE﹣AQ求出QE的长度,然后过点E作EP⊥BC于点P,则EP为点E到直线BC的距离,进而在Rt△QPE中求出PE的值在于7进行比较即可得到答案.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin2x+cos2(
sin2x+cos2( ![]() ﹣x)﹣
﹣x)﹣ ![]() (x∈R).
(x∈R).
(1)求函数f(x)在区间[0, ![]() ]上的最大值;
]上的最大值;
(2)在△ABC中,若A<B,且f(A)=f(B)= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{bn}的前n项和为Sn , 且对任意正整数n,都有 ![]() ;
;
(1)试证明数列{bn}是等差数列,并求其通项公式;
(2)如果等比数列{an}共有2017项,其首项与公比均为2,在数列{an}的每相邻两项ai与ai+1之间插入i个(﹣1)ibi(i∈N*)后,得到一个新数列{cn},求数列{cn}中所有项的和;
(3)如果存在n∈N* , 使不等式 ![]() 成立,若存在,求实数λ的范围,若不存在,请说明理由.
成立,若存在,求实数λ的范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2|x+2|﹣|x+1|,无穷数列{an}的首项a1=a.
(1)如果an=f(n)(n∈N*),写出数列{an}的通项公式;
(2)如果an=f(an﹣1)(n∈N*且n≥2),要使得数列{an}是等差数列,求首项a的取值范围;
(3)如果an=f(an﹣1)(n∈N*且n≥2),求出数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=lg(m2﹣2m﹣2)+(m2+3m+2)i,根据以下条件分别求实数m的值或范围.
(1)z是纯虚数;
(2)z对应的点在复平面的第二象限.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年上半年,股票投资人袁先生同时投资了甲、乙两只股票,其中甲股票赚钱的概率为 ![]() ,赔钱的概率是
,赔钱的概率是 ![]() ;乙股票赚钱的概率为
;乙股票赚钱的概率为 ![]() ,赔钱的概率为
,赔钱的概率为 ![]() .对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元. (Ⅰ)求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;
.对于甲股票,若赚钱则会赚取5万元,若赔钱则损失4万元;对于乙股票,若赚钱则会赚取6万元,若赔钱则损失5万元. (Ⅰ)求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;
(Ⅱ)试求袁先生2016年上半年同事投资甲、乙两只股票的总收益的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com