
【题目】已知函数f(x)=ex-e-x(x∈R,且e为自然对数的底数).
(1)判断函数f(x)的单调性与奇偶性;
(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切x∈R都成立?若存在,求出t;若不存在,请说明理由.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:
【题目】已知点A(l,2)在函数f(x)=ax3的图象上,则过点A的曲线C:y=f(x)的切线方程是( )
A. 6x﹣y﹣4=0 B. x﹣4y+7=0
C. 6x﹣y﹣4=0或x﹣4y+7=0 D. 6x﹣y﹣4=0或3x﹣2y+1=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1的中点,且FD⊥AC1,有下述结论:
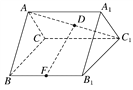
①AC1⊥BC;
②![]() =1;
=1;
③平面FAC1⊥平面ACC1A1;
④三棱锥D-ACF的体积为![]() .
.
其中正确结论的个数为( )
A. 1 B. 2
C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2018年春节前夕,![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
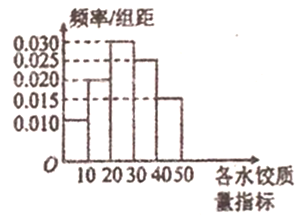
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,若
中,若![]() 是整数,且
是整数,且![]() (
(![]() ,且
,且![]() ).
).
(Ⅰ)若![]() ,
, ![]() ,写出
,写出![]() 的值;
的值;
(Ⅱ)若在数列![]() 的前2018项中,奇数的个数为
的前2018项中,奇数的个数为![]() ,求
,求![]() 得最大值;
得最大值;
(Ⅲ)若数列![]() 中,
中, ![]() 是奇数,
是奇数, ![]() ,证明:对任意
,证明:对任意![]() ,
, ![]() 不是4的倍数.
不是4的倍数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ln(x-1),其中a为常数.
(1)试讨论f(x)的单调区间;
(2)当a=![]() 时,存在x使得不等式
时,存在x使得不等式![]() 成立,求b的取值范围.
成立,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com