
【题目】已知函数f(x)=2sin(ωx),其中常数ω>0
(1)若y=f(x)在[﹣ ![]() ,
, ![]() ]上单调递增,求ω的取值范围;
]上单调递增,求ω的取值范围;
(2)令ω=2,将函数y=f(x)的图象向左平移 ![]() 个单位,再向上平移1个单位,得到函数y=g(x)的图象,区间[a,b](a,b∈R,且a<b)满足:y=g(x)在[a,b]上至少含有30个零点.在所有满足上述条件的[a,b]中,求b﹣a的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象,区间[a,b](a,b∈R,且a<b)满足:y=g(x)在[a,b]上至少含有30个零点.在所有满足上述条件的[a,b]中,求b﹣a的最小值.
【答案】
(1)解:∵函数y=f(x)在 ![]() 上单调递增,且ω>0,
上单调递增,且ω>0,
∴ ![]() ,且
,且 ![]() ,
,
解得 ![]() .
.
(2)解:f(x)=2sin2x,∴把y=f(x)的图象向左平移 ![]() 个单位,再向上平移1个单位,得到
个单位,再向上平移1个单位,得到 ![]() ,
,
∴函数y=g(x)= ![]() ,
,
令g(x)=0,得 ![]() ,或x=
,或x= ![]() (k∈Z).
(k∈Z).
∴相邻两个零点之间的距离为 ![]() 或
或 ![]() .
.
若b﹣a最小,则a和b都是零点,此时在区间[a,π+a],[a,2π+a],…,[a,mπ+a](m∈N*)分别恰有3,5,…,2m+1个零点,
所以在区间[a,14π+a]是恰有29个零点,从而在区间(14π+a,b]至少有一个零点,
∴ ![]() .
.
另一方面,在区间 ![]() 恰有30个零点,
恰有30个零点,
因此b﹣a的最小值为 ![]() .
.
【解析】(1)已知函数y=f(x)在 ![]() 上单调递增,且ω>0,利用正弦函数的单调性可得
上单调递增,且ω>0,利用正弦函数的单调性可得 ![]() ,且
,且 ![]() ,解出即可;(2)利用变换法则“左加右减,上加下减”即可得到g(x)=2
,解出即可;(2)利用变换法则“左加右减,上加下减”即可得到g(x)=2 ![]() .令g(x)=0,即可解出零点的坐标,可得相邻两个零点之间的距离.若b﹣a最小,则a和b都是零点,此时在区间[a,mπ+a](m∈N*)恰有2m+1个零点,所以在区间[a,14π+a]是恰有29个零点,从而在区间(14π+a,b]至少有一个零点,即可得到a,b满足的条件.进一步即可得出b﹣a的最小值.
.令g(x)=0,即可解出零点的坐标,可得相邻两个零点之间的距离.若b﹣a最小,则a和b都是零点,此时在区间[a,mπ+a](m∈N*)恰有2m+1个零点,所以在区间[a,14π+a]是恰有29个零点,从而在区间(14π+a,b]至少有一个零点,即可得到a,b满足的条件.进一步即可得出b﹣a的最小值.
【考点精析】根据题目的已知条件,利用正弦函数的单调性和函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数;图象上所有点向左(右)平移
上是减函数;图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为 ![]() ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为 ![]() .
.
(1)求椭圆的方程;
(2)设A,B分别为椭圆的左,右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若 ![]() =8,求k的值.
=8,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 关于直线
关于直线![]() 对称,且圆心在
对称,且圆心在![]() 轴上.
轴上.
(1)求![]() 的标准方程;
的标准方程;
(2)已经动点![]() 在直线
在直线![]() 上,过点
上,过点![]() 引
引![]() 的两条切线
的两条切线![]() 、
、![]() ,切点分别为
,切点分别为![]() .
.
①记四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值;
的最小值;
②证明直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近13年的宣传费
(单位:千元)的影响,对近13年的宣传费![]() 和年销售量
和年销售量![]()
![]() 数据作了初步处理,得到散点图及一些统计量的值.
数据作了初步处理,得到散点图及一些统计量的值.

由散点图知,按![]() 建立
建立![]() 关于
关于![]() 的回归方程是合理的.令
的回归方程是合理的.令![]() ,则
,则![]() ,经计算得如下数据:
,经计算得如下数据:
|
|
|
|
|
|
10.15 | 109.94 | 0.16 | -2.10 | 0.21 | 21.22 |
最小二乘法求线性回归方程系数公式
(Ⅰ)根据以上信息,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅱ)已知这种产品的年利润![]() 与
与![]() 的关系为
的关系为![]() .根据(1)的结果,求当年宣传费
.根据(1)的结果,求当年宣传费![]() 时,年利润的预报值是多少?
时,年利润的预报值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定常数c>0,定义函数f(x)=2|x+c+4|﹣|x+c|.数列a1 , a2 , a3 , …满足an+1=f(an),n∈N* .
(1)若a1=﹣c﹣2,求a2及a3;
(2)求证:对任意n∈N* , an+1﹣an≥c;
(3)是否存在a1 , 使得a1 , a2 , …,an , …成等差数列?若存在,求出所有这样的a1;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A在y轴正半轴上,点Pn在x轴上,其横坐标为xn , 且{xn} 是首项为1、公比为2的等比数列,记∠PnAPn+1=θn , n∈N* . 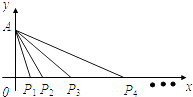
(1)若 ![]() ,求点A的坐标;
,求点A的坐标;
(2)若点A的坐标为(0,8 ![]() ),求θn的最大值及相应n的值.
),求θn的最大值及相应n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某公路AB一侧有一块空地△OAB,其中OA=3km,OB=3![]() km,∠AOB=90°.当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
km,∠AOB=90°.当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.

(1)若M在距离A点2km处,求点M,N之间的距离;
(2)为节省投入资金,人工湖△OMN的面积要尽可能小.试确定M的位置,使△OMN的面积最小,并求出最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com