
分析 (1)由等差数列前n项和公式、通项公式列出方程组,求出首项与公差,由此能求出an.
(2)推导出bn+1-bn=n,利用累加法求出bn=$\frac{1}{2}$n2-$\frac{1}{2}$n+1,从而$\frac{1}{{b}_{n}+n-1}$=$\frac{2}{{n}^{2}+n}$=2($\frac{1}{n}-\frac{1}{n+1}$),由此能求出数列{$\frac{1}{{{b_n}+n-1}}$}的前n项和Tn.
解答 (本小题满分12分)
解:(1)∵等差数列{an}的前n项和为Sn,且a2=2,S9=45,
∴$\left\{\begin{array}{l}{{a}_{1}+d=2}\\{9{a}_{1}+\frac{9×8}{2}d=45}\end{array}\right.$,解得a1=1,d=1,
an=1+(n-1)×1=n.…(4分)
(2)∵数列{bn}满足b1=l,$\frac{{{3^{{b_{n+1}}}}}}{{{3^{b_n}}}}$=${3^{a_n}}$(n∈N+),
∴bn+1-bn=n,
∴bn=b1+b2-b1+b3-b2+…+bn-bn-1
=1+1+2+3+…+(n-1)
=1+$\frac{n-1}{2}$(1+n-1)
=$\frac{1}{2}$n2-$\frac{1}{2}$n+1,
∴$\frac{1}{{b}_{n}+n-1}$=$\frac{2}{{n}^{2}+n}$=2($\frac{1}{n}-\frac{1}{n+1}$),
∴Tn=2(1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n}-\frac{1}{n+1}$)=2(1-$\frac{1}{n+1}$)=$\frac{2n}{n+1}$.
点评 本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
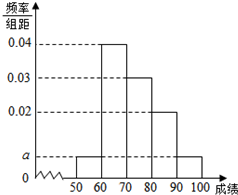 某校100名学生数学竞赛成绩的频率分布直方图如图所示,成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则该次数学成绩在[50,60)内的人数为( )
某校100名学生数学竞赛成绩的频率分布直方图如图所示,成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则该次数学成绩在[50,60)内的人数为( )| A. | 20 | B. | 15 | C. | 10 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
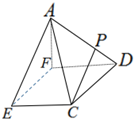 如图,在四棱锥A-CDEF中,四边形CDFE为直角梯形,CE∥DF,EF⊥FD,AF⊥平面CEFD,P为AD中点,EC=$\frac{1}{2}$FD.
如图,在四棱锥A-CDEF中,四边形CDFE为直角梯形,CE∥DF,EF⊥FD,AF⊥平面CEFD,P为AD中点,EC=$\frac{1}{2}$FD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com