
【题目】为了研究每周累计户外暴露时间是否足够(单位:小时)与近视发病率的关系,对某中学一年级![]() 名学生进行不记名问卷调查,得到如下数据:
名学生进行不记名问卷调查,得到如下数据:

(1)用样本估计总体思想估计该中学一年级学生的近视率;
(2)能否认为在犯错误的概率不超过![]() 的前提下认为不足够的户外暴露时间与近视有关系?
的前提下认为不足够的户外暴露时间与近视有关系?
附: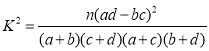 .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】小军的微信朋友圈参与了“微信运动”,他随机选取了40位微信好友(女20人,男20人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
5860 8520 7326 6798 7325 8430 3216 7453 11754 9860
8753 6450 7290 4850 10223 9763 7988 9176 6421 5980
男性好友走路的步数情况可分为五个类别(说明:a~b表示大于等于a,小于等于b)
A(0~2000步)1人, B(2001-5000步)2人, C(5001~8000步)3人,
D(8001-10000步)6人, E(10001步及以上)8人
若某人一天的走路步数超过8000步被系统认定为“健康型”否则被系统认定为“进步型”.
(I)访根据选取的样本数据完成下面的2×2列联表,并根据此判断能否有95%以上的把握认为“认定类型”与“性别”有关?
健康型 | 进步型 | 总计 | |
男 | 20 | ||
女 | 20 | ||
总计 | 40 |
(Ⅱ)如果从小军的40位好友中该天走路步数超过10000的人中随机抽取3人,设抽到女性好友X人,求X的分布列和数学期望![]() .
.
附:![]()
![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新中国成立70周年国庆阅兵庆典中,众多群众在脸上贴着一颗红心,以此表达对祖国的热爱之情,在数学中,有多种方程都可以表示心型曲线,其中有著名的笛卡尔心型曲线,如图,在直角坐标系中,以原点O为极点,x轴正半轴为极轴建立极坐标系.图中的曲线就是笛卡尔心型曲线,其极坐标方程为![]() (
(![]() ),M为该曲线上的任意一点.
),M为该曲线上的任意一点.
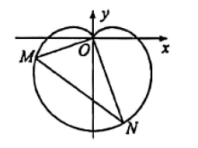
(1)当![]() 时,求M点的极坐标;
时,求M点的极坐标;
(2)将射线OM绕原点O逆时针旋转![]() 与该曲线相交于点N,求
与该曲线相交于点N,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 的左焦点为
的左焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() 使得直线
使得直线![]() 的斜率互为相反数?若存在,求出定点
的斜率互为相反数?若存在,求出定点![]() 的坐标;若不存在,也请说明理由.
的坐标;若不存在,也请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,△ABC是以AC为斜边的等腰直角三角形,△BCD是等边三角形.如图②,将△BCD沿BC折起,使平面BCD⊥平面ABC,记BC的中点为E,BD的中点为M,点F、N在棱AC上,且AF=3CF,C![]() .
.
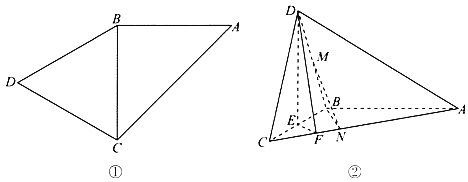
(1)试过直线MN作一平面,使它与平面DEF平行,并加以证明;
(2)记(1)中所作的平面为α,求平面α与平面BMN所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com