解:(1)由题意可得 p(x)=f(x)+g(x)=2x
2-(k+1)x+15-k 在(1,4)上有零点.
∴△=(k
2+2k+1)-8(15-k)≥0,解得 k≤-17,或 k≥7.
若p(x)在(1,4)上有唯一零点,则 p(1)p(4)=(16-2k)(43-5k)<0 ①,
或
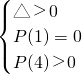
②,或
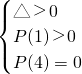
③,或
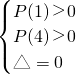
④.
解①得 8<k<
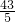
,解②得k=8,解③得k∈∅,解④可得 k=7.
若p(x)在(1,4)上有2个零点,则有
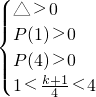
,解得 7<k<8.
综上可得,实数k的取值范围为[7,
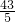
).
(2)函数
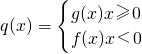
,即
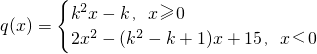
.
显然,k=0不满足条件,故k≠0.
当x≥0时,q(x)=k
2x-k∈[-k,+∞).
当x<0时,q(x)=2x
2-(k
2+k+1)x+15∈(15,+∞).
记A=[-k,+∞),记 B=(15,+∞).
①当x
2>0时,q(x)在(0,+∞)上是增函数,要使q(x
2)=q(x
1),则x
1<0,且A?B,
故-k≥15,解得 k≤-15.
②当x
2<0时,q(x)在(-∞,0)上是减函数,要使q(x
2)=q(x
1),则x
1>0,且B?A,
故-k≤15,解得 k≥-15.
综上可得,k=-5满足条件.
分析:(1)由题意可得p(x)=2x
2-(k+1)x+15-k 在(1,4)上有零点,分p(x)在(1,4)上有唯一零点和p(x)
在(1,4)上有2个零点,这两种情况,分别求出实数k的取值范围,再取并集,即得所求.
(2)根据q(x)的解析式可得k≠0,当x≥0时,求得q(x)的值域当x<0时,求得q(x) 的值域,当x
2>0时,
可得k≤-15;②当x
2<0时,可得k≥-15,结合①②可得k的值.
点评:本题主要考查函数的零点与方程的根的关系,函数的单调性的应用,体现了化归与转化、以及分类讨论的数学思想,
属于中档题.

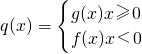 是否存在实数k,对任意给定的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得q(x2)=q(x1)?若存在,求出k的值;若不存在,请说明理由.
是否存在实数k,对任意给定的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得q(x2)=q(x1)?若存在,求出k的值;若不存在,请说明理由.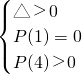 ②,或
②,或 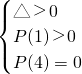 ③,或
③,或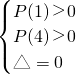 ④.
④.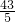 ,解②得k=8,解③得k∈∅,解④可得 k=7.
,解②得k=8,解③得k∈∅,解④可得 k=7.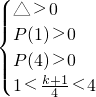 ,解得 7<k<8.
,解得 7<k<8.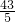 ).
).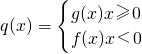 ,即
,即 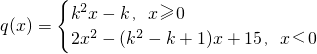 .
.
