
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,
是正方形,![]() 平面
平面![]() ,且
,且![]() ,点
,点![]() 为线段
为线段![]() 的中点.
的中点.
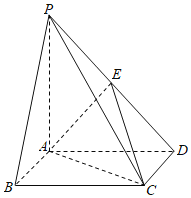
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的有( )
(1)若p∧q为假命题,则p、q均为假命题;
(2)“x=1”是“x2﹣3x+2=0”的充分不必要条件;
(3)若“p∨q”为假命题,则“¬p∧¬q”为真命题.
(4)命题“若x2﹣3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为降低汽车尾气的排放量,某厂生产甲乙两种不同型号的节排器,分别从甲乙两种节排器中各自抽取100件进行性能质量评估检测,综合得分情况的频率分布直方图如图所示.
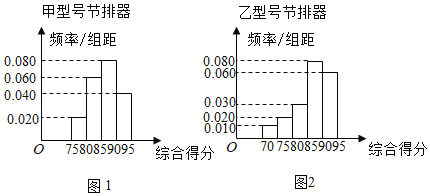
节排器等级及利润如表格表示,其中![]()
综合得分 | 节排器等级 | 节排器利润率 |
| 一级品 |
|
| 二级品 |
|
| 三级品 |
|
(1)若从这100件甲型号节排器按节排器等级分层抽样的方法抽取10件,再从这10件节排器中随机抽取3件,求至少有2件一级品的概率;
(2)视频率分布直方图中的频率为概率,用样本估计总体,则
①若从乙型号节排器中随机抽取3件,求二级品数![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
②从长期来看,骰子哪种型号的节排器平均利润较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,且4an+1﹣anan+1+2an=9(n∈N*).
(1)求a2,a3,a4;
(2)由(1)猜想{an}的通项公式an ;
(3)用数学归纳法证明(2)的结果.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,-2)、N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]()
![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)如图,动直线![]() :
: ![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点, ![]() 是椭圆
是椭圆![]() 上一点,直线
上一点,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,
, ![]() 是线段
是线段![]() 延长线上一点,且
延长线上一点,且![]() ,
, ![]() 的半径为
的半径为![]() ,
, ![]() 是
是![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .求
.求![]() 的最大值,并求取得最大值时直线
的最大值,并求取得最大值时直线![]() 的斜率.
的斜率.
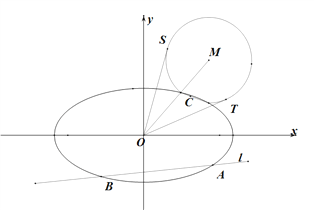
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com