Question

【题目】某班“数学兴趣小组”对函数y＝﹣x2+2|x|+1的图象和性质进行了探究，探究过程如下，请补充完整．

（1）自变量x的取值范围是全体实数，x与y的几组对应值列表如下：

x	…	﹣3	﹣	﹣2	﹣1	0	1	2		3	…
y	…	﹣2		m	2	1	2	1		﹣2	…

其中，m＝　　．

（2）根据上表数据，在如图所示的平面直角坐标系中描点，画出了函数图象的一部分，请画出该函数图象的另一部分．

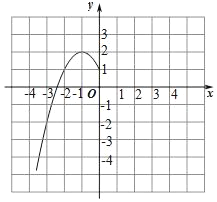
（3）观察函数图象，写出两条函数的性质．

（4）进一步探究函数图象发现：

①方程﹣x2+2|x|+1＝0有　　个实数根；

②关于x的方程﹣x2+2|x|+1＝a有4个实数根时，a的取值范围是　　．

Answer 1

【答案】（1）1；（2）答案见解析；（3）①函数的最大值是2，没有最小值；②当x＞1时，y随x的增大而减小；（答案不唯一）（4）①2；②1＜a＜2．

【解析】

（1）根据对称性或直接代数计算即可得答案；

（2）描点画出图形即可；

（3）可写函数的最大值和最小值问题，也可确定一个范围写增减性问题（答案不唯一）；

（4）①当y=0时，图象与x轴的交点有两个，则方程有2个实数根；②直线y=a与图象有4个交点，即表示方程有4个实根，据此结合图象确定a的范围即可．

（1）当时，，所以m=1，

故答案为：1；

（2）根据表格数据，描点画图如下：

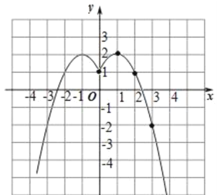
（3）根据图象可知，函数具有如下性质：①函数的最大值是2，没有最小值；②当x＞1时，y随x的增大而减小；（答案不唯一）

（4）①由图象可知：函数图象与x轴有两个交点，

所以方程﹣x2+2|x|+1＝0有2个实数根，

故答案为：2；

②方程﹣x2+2|x|+1＝a有4个实数根时，

即表示y＝a与图象有4个交点，

故由图象可知，a的取值范围是：1＜a＜2．

故答案为：1＜a＜2．