
【题目】已知△ABC的三个内角A、B、C所对的边分别为a,b,c,且4sin2 ![]() ﹣cos2A=
﹣cos2A= ![]()
(1)求角A的大小,
(2)若a= ![]() ,cosB=
,cosB= ![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】
(1)解:∵sin2 ![]() =
= ![]() [1﹣cos(B+C)]=
[1﹣cos(B+C)]= ![]() (1+cosA),cos2A=2cos2A﹣1
(1+cosA),cos2A=2cos2A﹣1
∴由4sin2 ![]() ﹣cos2A=
﹣cos2A= ![]() ,得(2cosA﹣1)2=0,解之得cosA=
,得(2cosA﹣1)2=0,解之得cosA= ![]()
∵A是三角形的内角,∴A=60°
(2)解:由cosB= ![]() ,得sinA=
,得sinA= ![]() =
= ![]()
∵ ![]() ,∴b=
,∴b= ![]() =
= ![]()
又∵sinC=sin(A+B)=sinAcosB+cosAsinB= ![]()
∴△ABC的面积为S= ![]() absinC=
absinC= ![]() ×
× ![]() =
= ![]()
【解析】(1)利用三角恒等变换公式和诱导公式,化简已知等式得到(2cosA﹣1)2=0,解之得cosA= ![]() ,结合A是三角形的内角可得A=60°;(2)算出sinA=
,结合A是三角形的内角可得A=60°;(2)算出sinA= ![]() =
= ![]() ,结合正弦定理算出b=
,结合正弦定理算出b= ![]() =
= ![]() .利用诱导公式与两角和的正弦公式算出sinC=sin(A+B)=
.利用诱导公式与两角和的正弦公式算出sinC=sin(A+B)= ![]() ,最后利用正弦定理的面积公式即可算出△ABC的面积.
,最后利用正弦定理的面积公式即可算出△ABC的面积.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的函数y=f(x)是减函数,且对任意的a∈R,都有f(﹣a)+f(a)=0,若x、y满足不等式f(x2﹣2x)+f(2y﹣y2)≤0,则当1≤x≤4时,x﹣3y的最大值为( )
A.10
B.8
C.6
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱 ![]() 中,侧面
中,侧面![]() 和侧面
和侧面![]() 都是矩形,
都是矩形, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() 分别为
分别为![]() 的中点.
的中点.
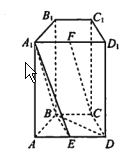
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
(3)若![]() 平面
平面![]() ,求棱
,求棱![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知美国苹果公司生产某款iPhone手机的年固定成本为40万美元,每生产1万只还需另投入16万美元.设苹果公司一年内共生产该款iPhone手机x万只并全部销售完,每万只的销售收入为R(x)万美元,且R(x)=
(1)写出年利润W(万美元)关于年产量x(万只)的函数解析式;
(2)当年产量为多少万只时,苹果公司在该款iPhone手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示. ![]() 是等腰梯形,
是等腰梯形, ![]() 米,
米, ![]() (
(![]() 在
在![]() 的延长线上,
的延长线上, ![]() 为锐角). 圆
为锐角). 圆![]() 与
与![]() 都相切,且其半径长为
都相切,且其半径长为![]() 米.
米. ![]() 是垂直于
是垂直于![]() 的一个立柱,则当
的一个立柱,则当![]() 的值设计为多少时,立柱
的值设计为多少时,立柱![]() 最矮?
最矮?
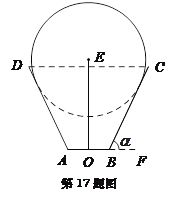
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
(1)求证:平面ABC1⊥平面A1ACC1;
(2)设D是线段BB1的中点,求三棱锥D﹣ABC1的体积.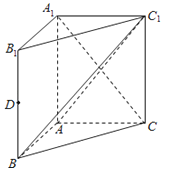
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com