
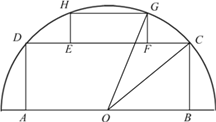
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池ABCD及其矩形附属设施EFGH,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为O,半径为R,矩形的一边AB在直径上,点C、D、G、H在圆周上,E、F在边CD上,且![]() ,设
,设![]()
(1)记游泳池及其附属设施的占地面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)当![]() 为何值时,能符合园林局的要求?
为何值时,能符合园林局的要求?
【答案】(1)![]() ;(2)当
;(2)当![]() 满足
满足![]() 时,符合园林局要求.
时,符合园林局要求.
【解析】试题分析:(1)由圆的性质可得, ![]() ,
, ![]() ,由
,由![]() 为等边三角形,
为等边三角形,
可得, ![]() ,
, ![]() ,所以
,所以![]() ,结合三角形面积公式可得结果 ;(2)由
,结合三角形面积公式可得结果 ;(2)由![]() 可得极值点
可得极值点![]() 满足,
满足, ![]() ,利用导数研究函数的单调性可得当
,利用导数研究函数的单调性可得当![]() 时
时![]() 是单调减函数,当
是单调减函数,当![]() 时,
时, ![]() 是单调增函数,所以当
是单调增函数,所以当![]() 时,
时, ![]() 取得最小值.
取得最小值.
试题解析:(1)由题意, ![]() ,
, ![]() ,且
,且![]() 为等边三角形,
为等边三角形,
所以, ![]() ,
, ![]() ,
,
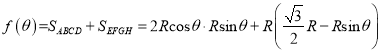
![]() ,
, 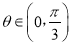 .
.
(2)要符合园林局的要求,只要![]() 最小,
最小,
由(1)知, ![]()
令![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
令![]() .
.
当![]() 时,
时, ![]() 是单调减函数,当
是单调减函数,当![]() 时,
时, ![]() 是单调增函数,所以当
是单调增函数,所以当![]() 时,
时, ![]() 取得最小值.
取得最小值.
答:当![]() 满足
满足![]() 时,符合园林局要求.
时,符合园林局要求.
思路点睛】本题主要考查阅读能力、数学建模能力和化归思想以及导数在解决实际问题中的应用,属于难题. 与实际应用相结合的题型也是高考命题的动向,这类问题的特点是通过现实生活的事例考查书本知识,解决这类问题的关键是耐心读题、仔细理解题,只有吃透题意,才能将实际问题转化为数学模型进行解答.理解本题题意的关键是:将游泳池及其附属设施的占地面积为关于![]() 的函数,然后利用导数解答.
的函数,然后利用导数解答.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
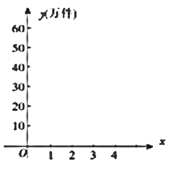
【题目】某公司为了准确地把握市场,做好产品生产计划,对过去四年的数据进行整理得到了第![]() 年与年销量
年与年销量![]() (单位:万件)之间的关系如下表:
(单位:万件)之间的关系如下表:

(1)在图中画出表中数据的散点图;
(2)根据散点图选择合适的回归模型拟合![]() 与
与![]() 的关系(不必说明理由);
的关系(不必说明理由);
(3)建立![]() 关于
关于![]() 的回归方程,预测第5年的销售量.
的回归方程,预测第5年的销售量.
附注:参考公式:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【题目】【2018江西莲塘一中、临川二中高三上学期第一次联考】二次函数![]() 的图象过原点,对
的图象过原点,对![]() ,恒有
,恒有![]() 成立,设数列
成立,设数列![]() 满足
满足![]() .
.
(I)求证:对![]() ,恒有
,恒有![]() 成立;
成立;
(II)求函数![]() 的表达式;
的表达式;
(III)设数列![]() 前
前![]() 项和为
项和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,函数
,函数![]() 的图像与函数
的图像与函数![]() 的图像相切,求
的图像相切,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函数
,函数![]() 满足对任意
满足对任意![]() ,都有
,都有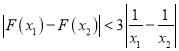 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() ,函数
,函数![]() ,且
,且![]() 有两个极值点
有两个极值点![]() ,其中
,其中![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 既有一个极小值又有一个极大值,求
既有一个极小值又有一个极大值,求![]() 的取值范围;
的取值范围;
(3)若存在![]() ,使得当
,使得当![]() 时,
时, ![]() 的值域是
的值域是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(1)若![]() =
= ![]() ,求证:曲线
,求证:曲线![]() 上的任意一点处的切线与直线
上的任意一点处的切线与直线![]() 和直线
和直线![]() 围成的三角形面积为定值;
围成的三角形面积为定值;
(2)若![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对于定义域内的任意
对于定义域内的任意![]() 都成立;
都成立;
(3)在(2)的条件下,若方程![]() 有三个解,求实数
有三个解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
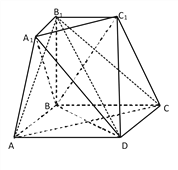
【题目】如图所示的几何体是由棱台![]() 和棱锥
和棱锥![]() 拼接而成的组合体,其底面四边形
拼接而成的组合体,其底面四边形![]() 是边长为
是边长为![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求证:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com