
 和
和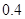 ,那么至少有一个人解对的概率为( )
,那么至少有一个人解对的概率为( )A. | B. | C. | D.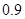 |
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中数学 来源:不详 题型:解答题
| | 燃料电池轿车 | 混合动力轿车 | 氢能源动力轿车 |
| 标准型 | 100 | 200 |  |
| 豪华型 | 200 | 300 | 500 |
 的值.
的值. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
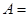 “取到的2个球☆个数之和为奇数”,事件
“取到的2个球☆个数之和为奇数”,事件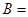 “取到的2个球同色”,则
“取到的2个球同色”,则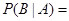 ( )
( ) A.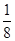 | B. | C. | D.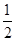 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
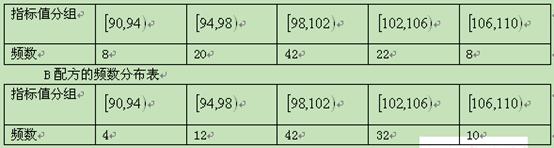
 2列联表,问是否有99
2列联表,问是否有99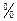 的把握认为“A配方与B配方的质量有差异”。
的把握认为“A配方与B配方的质量有差异”。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.A与B是互斥而非对立事件 | B.A与B是对立事件 |
| C.B与C是互斥而非对立事件 | D.B与C是对立事件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
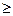 10的概率;
10的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
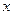 的不等式
的不等式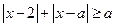 在
在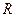 上恒成立,则
上恒成立,则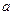 的最大值是1;
的最大值是1;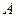 :“甲、乙中至少一人击中目标”与事件
:“甲、乙中至少一人击中目标”与事件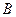 :“甲,乙都没有击中目标”是相互独立事件。
:“甲,乙都没有击中目标”是相互独立事件。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
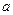 万元,年利率为
万元,年利率为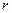 ,按复利计算,从2011年末开始,每年末偿还一定金额,计划第5年底还清,则每年应偿还的金额数为 万元.
,按复利计算,从2011年末开始,每年末偿还一定金额,计划第5年底还清,则每年应偿还的金额数为 万元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com