练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某租赁公司拥有汽车100辆，当每辆车的月租金为3000元时，可全部租出.若每辆车的月租金每增加50元，未租出的车将会增加一辆，租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元.

    （1）当每辆车的月租金定为3600元时，能租出多少辆车？

    （2）当每辆车的月租金定为多少元时，租赁公司的月收益最大，最大月收益是多少？

    【答案】见解析

    【解析】（1）当每辆车的月租金定为元时，未租出的车为辆，（2分）

    ，

    所以租出了辆车.（4分）

    （2）设每辆车的月租金定为元，

    则租凭公司的月收益为，（6分）

    整理得，（8分）

    所以当时，最大，其最大值为，（10分）

    答：当每辆车的月租金定为元时，租赁公司的月收益最大，最大月收益是元．（12分）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x|（x﹣a），a为实数．

    （1）若函数f（x）为奇函数，求实数a的值；

    （2）若函数f（x）在[0，2]为增函数，求实数a的取值范围；

    （3）是否存在实数a（a＜0），使得f（x）在闭区间上的最大值为2，若存在，求出a的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线在处的切线方程为．

    （1）求的值；

    （2）若对任意恒成立，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合M＝{x|x＝m＋，m∈Z}，N＝{x|x＝－，n∈Z}，P＝{x|x＝＋，p∈Z}，试确定M，N，P之间的关系.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知：函数且.

    （1）求定义域；

    （2）判断的奇偶性，并说明理由；

    （3）求使的的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数是定义在R上的奇函数，其中为自然对数的底数.

    （1）求实数的值；

    （2）若存在，使得不等式成立，求实数的取值范围；

    （3）若函数在上不存在最值，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于定义域为的函数，若同时满足下列条件：

    ①在内单调递增或单调递减；

    ②存在区间，使在上的值域为；那么把（）叫闭函数.

    （1）求闭函数符合条件②的区间；

    （2）判断函数是否为闭函数？并说明理由；

    （3）判断函数是否为闭函数？若是闭函数，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

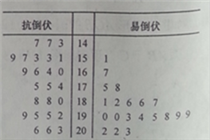
    【题目】为了打好脱贫攻坚战，某贫困县农科院针对玉米种植情况进行调研，力争有效的改良玉米品种，为农民提供技术支.现对已选出的一组玉米的茎高进行统计，获得茎叶图如右图（单位：厘米），设茎高大于或等于180厘米的玉米为高茎玉米，否则为矮茎玉米.

    （1）完成列联表，并判断是否可以在犯错误的概率不超过1%的前提下，认为抗倒伏与玉米矮茎有关？

    （2）为了改良玉米品种，现采用分层抽样的方法从抗倒伏的玉米中抽出5株，再从这5株玉米中选取2株进行杂交试验，选取的植株均为矮茎的概率是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在D上的函数，若满足： ，都有成立，则称是D上的有界函数，其中M称为函数的上界.

    （I）设，证明： 在上是有界函数，并写出所有上界的值的集合；

    （II）若函数在上是以3为上界的有界函数，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案