
【题目】已知集合M={x|x=m+![]() ,m∈Z},N={x|x=
,m∈Z},N={x|x=![]() -
-![]() ,n∈Z},P={x|x=
,n∈Z},P={x|x=![]() +
+![]() ,p∈Z},试确定M,N,P之间的关系.
,p∈Z},试确定M,N,P之间的关系.
【答案】M![]() P=N.
P=N.
【解析】试题分析:M={x|x=m+![]() ,m∈Z}={x|x=
,m∈Z}={x|x=![]() ,m∈Z}={x|x=
,m∈Z}={x|x=![]() ,m∈Z}M表示3的偶数倍加1除以6的数;N={x|x=
,m∈Z}M表示3的偶数倍加1除以6的数;N={x|x=![]() ,n∈Z}={x|x=
,n∈Z}={x|x=![]() ,n∈Z}
,n∈Z}
={x|x=![]() ,n-1∈Z},N表示3的整数倍加1除以6的数;P={x|x=
,n-1∈Z},N表示3的整数倍加1除以6的数;P={x|x=![]() +
+![]() ,p∈Z}={x|x=
,p∈Z}={x|x=![]() ,p∈Z},P表示3的整数倍加1除以6的数即可得出结论.
,p∈Z},P表示3的整数倍加1除以6的数即可得出结论.
试题解析:
∵M={x|x=m+![]() ,m∈Z}
,m∈Z}
={x|x=![]() ,m∈Z}={x|x=
,m∈Z}={x|x=![]() ,m∈Z},
,m∈Z},
N={x|x=![]() ,n∈Z}={x|x=
,n∈Z}={x|x=![]() ,n∈Z}
,n∈Z}
={x|x=![]() ,n-1∈Z},
,n-1∈Z},
P={x|x=![]() +
+![]() ,p∈Z}={x|x=
,p∈Z}={x|x=![]() ,p∈Z},
,p∈Z},
比较3×2m+1,3(n-1)+1与3p+1可知,3(n-1)+1与3p+1表示的数完全相同,
∴N=P,3×2m+1只相当于3p+1中当p为偶数时的情形,
∴M![]() P=N.
P=N.
综上可知M![]() P=N.
P=N.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() ,曲线
,曲线![]() :
: ![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线![]() ,
, ![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ,
, ![]() )分别交
)分别交![]() ,
, ![]() 于
于![]() ,
, ![]() 两点,当
两点,当![]() 取何值时,
取何值时, ![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为自然对数的底数),
为自然对数的底数),![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)当![]() 时,求证:
时,求证:![]() ;
;
(Ⅱ)是否存在正整数![]() ,使得
,使得![]() 对一切
对一切![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点O为坐标原点,椭圆E:![]() (a≥b>0)的右顶点为A,上顶点为B,过点O且斜率为
(a≥b>0)的右顶点为A,上顶点为B,过点O且斜率为![]() 的直线与直线AB相交M,且
的直线与直线AB相交M,且![]() .
.
(Ⅰ)求椭圆E的离心率e;
(Ⅱ)PQ是圆C:(x-2)2+(y-1)2=5的一条直径,若椭圆E经过P,Q两点,求椭圆E的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
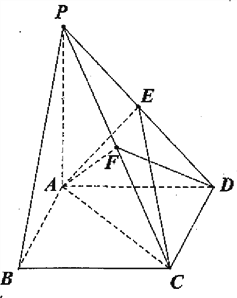
【题目】如图,四棱锥P—ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)若底面ABCD为正方形,![]() ,求二面角C—AF—D大小.
,求二面角C—AF—D大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《国务院关于修改〈中华人民共和国个人所得税法实施条例〉的决定》已于2008年3月1日起施行,个人所得税税率表如下:
级数 | 全月应纳税所得额 | 税率 |
1 | 不超过500元的部分 | 5% |
2 | 超过500至2 000元的部分 | 10% |
3 | 超过2 000元至5 000元的部分 | 15% |
… | … | … |
9 | 超过100 000元的部分 | 45% |
注:本表所示全月应纳税所得额为每月收入额减去2 000元后的余额.
(1)若某人2008年4月份的收入额为4 200元,求该人本月应纳税所得额和应纳的税费;
(2)设个人的月收入额为x元,应纳的税费为y元.当0<x≤3 600时,试写出y关于x的函数关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.若每辆车的月租金每增加50元,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大,最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产某种产品时的能耗y与产品件数x之间的关系式为y=ax+![]() .且当x=2时,y=100;当x=7时,y=35.且此产品生产件数不超过20件.
.且当x=2时,y=100;当x=7时,y=35.且此产品生产件数不超过20件.
(1)写出函数y关于x的解析式;
(2)用列表法表示此函数,并画出图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】幂函数f(x)=x3m-5(m∈N)在(0,+∞)上是减函数,且f(-x)=f(x),则m可能等于( )
A. 0 B. 1
C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com