Question

【题目】已知函数f（x）=|x|（x﹣a），a为实数．

（1）若函数f（x）为奇函数，求实数a的值；

（2）若函数f（x）在[0，2]为增函数，求实数a的取值范围；

（3）是否存在实数a（a＜0），使得f（x）在闭区间上的最大值为2，若存在，求出a的值；若不存在，请说明理由．

Answer 1

【答案】(1) a=0．（2）a≤0（3）a=﹣3．

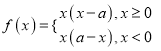【解析】试题分析：（1）因为f（x）为奇函数，所以f（﹣x）=﹣f（x），根据函数解析式，化简式子得2a|x|=0对任意x∈R恒成立，求得 ；（2）当 时，f（x）=|x|（x﹣a）可去掉绝对值号得f（x）=x（x﹣a），其对称轴为 ，要使函数f（x）在[0，2]上单调递增，由二次函数的图像可得 ，求 的范围。（3）当 时， 的解析式去掉绝对值号可得 ，因为f（x）在闭区间上的最大值为2，由特殊值 ，限定 的范围，因为函数的对称轴为 ，因为a＜0，所以函数在（0，+∞）上递增，所以，所以必在区间[﹣1，0]上取最大值2，讨论函数在[﹣1，0]上的单调性，最大值等于2，可求实数 的值。

试题解析：（1）因为奇函数f（x）定义域为R，

所以f（﹣x）=﹣f（x）对任意x∈R恒成立，

即|﹣x|（﹣x﹣a）=﹣|x|（x﹣a），即|x|（﹣x﹣a+x﹣a）=0，

即2a|x|=0对任意x∈R恒成立，

所以a=0．

（2）因为x∈[0，2]，所以f（x）=x（x﹣a），

显然二次函数的对称轴为，由于函数f（x）在[0，2]上单调递增，

所以，

即a≤0（若分a＜0，a=0，a＞0三种情况讨论即可）

（3）∵a＜0，，

∴f（﹣1）=﹣1﹣a≤2，∴﹣a≤3（先用特殊值约束范围）

∴，f（x）在（0，+∞）上递增，

∴f（x）必在区间[﹣1，0]上取最大值2．

当，即a＜﹣2时，则f（﹣1）=2，a=﹣3成立

当，即0＞a≥﹣2时，，则（舍）

综上，a=﹣3．