(理)设函数f(x)=(x+1)ln(x+1).
(1)求f(x)的单调区间;
(2)若对所有的x≥0,均有f(x)≥ax成立,求实数a的取值范围.
分析:(1)先求导,得到f'(x),分别令f'(x)>0,f'(x)<0得到递增和递减区间.
(2)令g(x)=(x+1)ln(x+1)-ax,注意到g(0)=0,则“不等式f(x)≥ax在x≥0时恒成立”等价于“g(x)≥g(0)在x≥0时恒成立”
通过求导研究函数g(x)的单调性和极值,从而画出函数图象,结合着g(0)=0,得到a的范围.
解答: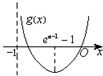
解:(1)由f'(x)=ln(x+1)+1≥0得
x≥-1,∴f(x)的增区间为
[-1,+∞),减区间为
(-1,-1].
(2)令g(x)=(x+1)ln(x+1)-ax.“不等式f(x)≥ax在x≥0时恒成立”?“g(x)≥g(0)在x≥0时恒成立.”g'(x)=ln(x+1)+1-a=0?x=e
a-1-1.
当x∈(-1,e
a-1-1)时,g'(x)<0,g(x)为减函数.
当x∈(e
a-1-1,+∞)时,g'(x)>0,g(x)为增函数.
“g(x)≥0在x≥0时恒成立”?“e
a-1-1≤0”,即e
a-1≤e
0,即a-1≤0,即a≤1.
故a的取值范围是(-∞,1].
点评:本题的第一小问是常规题,即利用导数研究函数的单调性,极值和最值.第二小问的转化,令g(x)=(x+1)ln(x+1)-ax,注意到g(0)=0,则“不等式f(x)≥ax在x≥0时恒成立”等价于“g(x)≥0在x≥0时恒成立”比较巧妙,避免了繁杂的分类讨论,使得问题更快地解决.

 解:(1)由f'(x)=ln(x+1)+1≥0得x≥
解:(1)由f'(x)=ln(x+1)+1≥0得x≥
