
【题目】已知函数f(x)=|lgx|﹣( ![]() )x有两个零点x1 , x2 , 则有( )
)x有两个零点x1 , x2 , 则有( )
A.x1x2<0
B.x1x2=1
C.x1x2>1
D.0<x1x2<1
【答案】D
【解析】解:f(x)=|lgx|﹣( ![]() )x有两个零点x1 , x2
)x有两个零点x1 , x2
即y=|lgx|与y=2﹣x有两个交点
由题意x>0,分别画y=2﹣x和y=|lgx|的图象
发现在(0,1)和(1,+∞)有两个交点
不妨设 x1在(0,1)里 x2在(1,+∞)里
那么 在(0,1)上有 2﹣x1=﹣lgx1 , 即﹣2﹣x1=lgx1…①
在(1,+∞)有2﹣x2=lg x2…②
①②相加有2﹣x2﹣2﹣x1=lgx1x2
∵x2>x1 , ∴2﹣x2<2﹣x1 即2﹣x2﹣2﹣x1<0
∴lgx1x2<0
∴0<x1x2<1
故选D.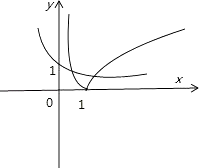
先将f(x)=|lgx|﹣( ![]() )x有两个零点转化为y=|lgx|与y=2﹣x有两个交点,然后在同一坐标系中画出两函数的图象得到零点在(0,1)和(1,+∞)内,即可得到﹣2﹣x1=lgx1和2﹣x2=lg x2 , 然后两式相加即可求得x1x2的范围.
)x有两个零点转化为y=|lgx|与y=2﹣x有两个交点,然后在同一坐标系中画出两函数的图象得到零点在(0,1)和(1,+∞)内,即可得到﹣2﹣x1=lgx1和2﹣x2=lg x2 , 然后两式相加即可求得x1x2的范围.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
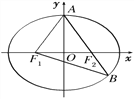
【题目】如图,F1,F2分别是椭圆![]() 的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)已知△AF1B的面积为![]() ,求椭圆C的方程.
,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x3+ax2+bx+c图像上的点P(1,f(1))处的切线方程为y=﹣3x+1.
(1)若函数f(x)在x=﹣2时有极值,求f(x)的表达式;
(2)函数f(x)在区间[﹣2,0]上单调递增,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+)(A>0,ω>0)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=π时,y有最大值3,当x=6π时,y有最小值﹣3.
(1)求此函数解析式;
(2)写出该函数的单调递增区间;
(3)是否存在实数m,满足不等式Asin( ![]() )>Asin(
)>Asin( ![]() )?若存在,求出m值(或范围),若不存在,请说明理由.
)?若存在,求出m值(或范围),若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了四个类比推理: (1.)由“若a,b,c∈R则(ab)c=a(bc)”类比推出“若a,b,c为三个向量则( ![]()
![]() )
) ![]() =
= ![]() (
( ![]()
![]() )”;
)”;
(2.)“a,b为实数,若a2+b2=0则a=b=0”类比推出“z1 , z2为复数,若 ![]() ”;
”;
(3.)“在平面内,三角形的两边之和大于第三边”类比推出“在空间中,四面体的任意三个面的面积之和大于第四个面的面积”;
(4.)“在平面内,过不在同一条直线上的三个点有且只有一个圆”类比推出“在空间中,过不在同一个平面上的四个点有且只有一个球”.
上述四个推理中,结论正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于函数f(x),若在定义域内存在实数x,满足f(﹣x)=﹣f(x),则称f(x)为“局部奇函数”.
(1)已知二次函数f(x)=ax2+2x﹣4a(a∈R),试判断f(x)是否为定义域R上的“局部奇函数”?若是,求出满足f(﹣x)=﹣f(x)的x的值;若不是,请说明理由;
(2)若f(x)=2x+m是定义在区间[﹣1,1]上的“局部奇函数”,求实数m的取值范围.
(3)若f(x)=4x﹣m2x+1+m2﹣3为定义域R上的“局部奇函数”,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() 是定义在区间(﹣1,1)上的奇函数,且f(2)=
是定义在区间(﹣1,1)上的奇函数,且f(2)= ![]() ,
,
(1)确定函数f(x)的解析式;
(2)用定义法证明f(x)在区间(﹣1,1)上是增函数;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com