
已知函数f(x)=ax3+x2+bx(其中常数a,b∈R),g(x)=f(x)+f ′(x)是奇函数.
(1)求f(x)的表达式;
(2)讨论g(x)的单调性,并求g(x)在区间[1,2]上的最大值与最小值.
解:(1)由题意得f ′(x)=3ax2+2x+b,
因此g(x)=f(x)+f ′(x)=ax3+(3a+1)x2+(b+2)x+b.
因为函数g(x)是奇函数,所以g(-x)=-g(x),
即对任意实数x,有a(-x)3+(3a+1)(-x)2+(b+2)(-x)+b=-[ax3+(3a+1)x2+(b+2)x+b],
从而3a+1=0,b=0,解得a=-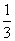 ,b=0,
,b=0,
因此f(x)的表达式为f(x)=-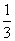 x3+x2.
x3+x2.
(2)由(1)知g(x)=-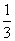 x3+2x,
x3+2x,
所以g′(x)=-x2+2.
令g′(x)=0,解得x1=-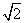 ,x2=
,x2=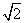 .
.
则当x<-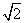 或x>
或x>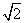 时,g′(x)<0,从而g(x)在区间(-∞,-
时,g′(x)<0,从而g(x)在区间(-∞,-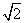 ],[
],[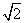 ,+∞)上是减函数;
,+∞)上是减函数;
当-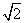 <x<
<x<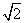 时,g′(x)>0,从而g(x)在区间[-
时,g′(x)>0,从而g(x)在区间[-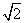 ,
,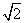 ]上是增函数.
]上是增函数.
由上述讨论知,g(x)在区间[1,2]上的最大值与最小值只能在x=1,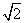 ,2时取得,
,2时取得,
而g(1)=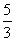 ,g(
,g(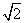 )=
)=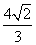 ,g(2)=
,g(2)=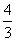 ,
,
因此g(x)在区间[1,2]上的最大值为g(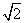 )=
)=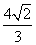 ,最小值为g(2)=
,最小值为g(2)=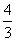 .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
已知a,b为两个不相等的实数,集合M={a2-4a,-1},N={b2-4b+1,-2},f:x→x表示把M中的元素x映射到集合N中仍为x,则a+b等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在淘宝网上,某店铺专卖当地某种特产,由以往的经验表明,不考虑其他因素,该特产每日的销售量y(单位:千克)与销售价格x(单位:元/千克,1<x≤5)满足:当1<x≤3时,y=a(x-3)2+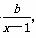 ,(a,b为常数);当3<x≤5时,y=-70x+490,已知当销售价格为2元/千克时,每日可售出该特产700千克;当销售价格为3元/千克时,每日可售出该特产150千克.
,(a,b为常数);当3<x≤5时,y=-70x+490,已知当销售价格为2元/千克时,每日可售出该特产700千克;当销售价格为3元/千克时,每日可售出该特产150千克.
(1)求a,b的值,并确定y关于x的函数解析式;
(2)若该特产的销售成本为1元/千克,试确定销售价格x的值,使店铺每日销售该特产所获利润f(x)最大(x精确到0.01元/千克).
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)满足x2f ′(x)+2xf(x)=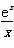 , f(2)=
, f(2)=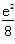 ,则x>0时,f(x)( )
,则x>0时,f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值也无极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x-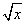 -1,g(x)=x+2x,h(x)=x+ln x的零点分别为x1,x2,x3,则( )
-1,g(x)=x+2x,h(x)=x+ln x的零点分别为x1,x2,x3,则( )
A.x1<x2<x3 B.x2<x1<x3
C.x3<x1<x2 D.x2<x3<x1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com