
(本题满分12分)已知函数 (
(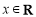 ),
),
(1)求函数 的最小值;
的最小值;
(2)已知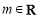 ,
, :关于
:关于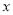 的不等式
的不等式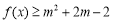 对任意
对任意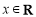 恒成立;
恒成立;
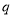 :函数
:函数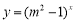 是增函数.若“
是增函数.若“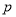 或
或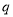 ”为真,“
”为真,“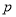 且
且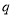 ”为假,求实数
”为假,求实数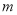 的取值范围.
的取值范围.
(1)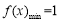 (2)实数
(2)实数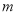 的取值范围是
的取值范围是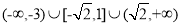 .
.
【解析】
试题分析:(1)求函数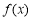 的最小值,这是分段函数的最值问题,分段函数的最小值可以分段求最小值,然后比较谁最小即可,也可采用数形结合,即作出函数的图象,由函数图像观察出最小值;(2)若“
的最小值,这是分段函数的最值问题,分段函数的最小值可以分段求最小值,然后比较谁最小即可,也可采用数形结合,即作出函数的图象,由函数图像观察出最小值;(2)若“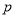 或
或 ”为真,“
”为真,“ 且
且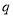 ”为假,求实数
”为假,求实数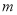 的取值范围.这是两个命题有且只有一个为真问题,做这类问题,可分两种情况处理,
的取值范围.这是两个命题有且只有一个为真问题,做这类问题,可分两种情况处理,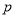 真,
真, 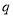 假,与
假,与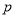 假,
假, 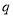 真,分别求出实数
真,分别求出实数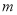 的取值范围,然后取并集即可.也可两个命题都为真时,分别求出范围,求两个集合的并集与交集,并集中出去交集部分,剩下即为所求.
的取值范围,然后取并集即可.也可两个命题都为真时,分别求出范围,求两个集合的并集与交集,并集中出去交集部分,剩下即为所求.
试题解析:(1) , 作出图像可知,
, 作出图像可知,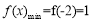 (4分)
(4分)
(2)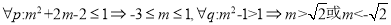 (8分)
(8分)
∵“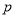 或
或 ”为真,“
”为真,“ 且
且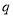 ”为假,
”为假, 当
当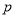 真,
真, 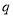 假时,则
假时,则 ,解得
,解得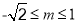 (10分)
(10分)
当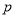 假,
假, 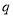 真时,则
真时,则 ,解得
,解得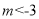 或
或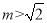 ,
,
故实数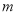 的取值范围是
的取值范围是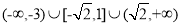 . (12分)
. (12分)
考点:逻辑连接词.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:2015届福建省八县(市高三上学期半期联考文科数学试卷(解析版) 题型:选择题
已知函数 的导函数图象如图所示,若
的导函数图象如图所示,若 是以角
是以角 为钝角的钝角三角形,则一定成立的是( )
为钝角的钝角三角形,则一定成立的是( )

A.
B.
C.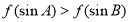
D.
查看答案和解析>>
科目:高中数学 来源:2015届湖南省衡阳市高三上学期五校联考理科数学试卷(解析版) 题型:解答题
(本小题满分13分)设函数 有两个极值点
有两个极值点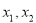 ,且
,且 .
.
(1)求实数 的取值范围;
的取值范围;
(2)讨论函数 的单调性;
的单调性;
(3)若对任意的 ,都有
,都有 成立,求实数
成立,求实数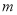 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com