
【题目】如图是抛物线形拱桥,当水面在l时,拱顶离水面4米,水面宽8米.水位上升1米后,水面宽为( ) 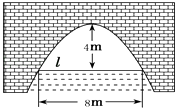
A.![]() 米
米
B.2 ![]() 米
米
C.3 ![]() 米
米
D.4 ![]() 米
米
【答案】D
【解析】解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点, 
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半4米,抛物线顶点C坐标为(0,4),
通过以上条件可设顶点式y=ax2+4,其中a可通过代入A点坐标(﹣4,0),
到抛物线解析式得出:a=﹣ ![]() ,所以抛物线解析式为y=﹣
,所以抛物线解析式为y=﹣ ![]() x2+4,
x2+4,
当水面上升1米,通过抛物线在图上的观察可转化为:
当y=1时,对应的抛物线上两点之间的距离,也就是直线y=1与抛物线相交的两点之间的距离,
可以通过把y=1代入抛物线解析式得出:
1=﹣ ![]() x2+4,
x2+4,
解得:x=±2 ![]() ,
,
所以水面宽度增加到4 ![]() 米,
米,
故选:D.


科目:高中数学 来源: 题型:
【题目】已知函数  ,设F(x)=x2f(x),则F(x)是( )
,设F(x)=x2f(x),则F(x)是( )
A.奇函数,在(﹣∞,+∞)上单调递减
B.奇函数,在(﹣∞,+∞)上单调递增
C.偶函数,在(﹣∞,0)上递减,在(0,+∞)上递增
D.偶函数,在(﹣∞,0)上递增,在(0,+∞)上递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg).其频率分布直方图如下:

(1)设两种养殖方法的箱产量相互独立,记A表示事件:“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附: ,
, 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】佛山某中学高三(1)班排球队和篮球队各有10名同学,现测得排球队10人的身高(单位:cm)分别是:162、170、171、182、163、158、179、168、183、168,篮球队10人的身高(单位:cm)分别是:170、159、162、173、181、165、176、168、178、179.
(1)请把两队身高数据记录在如图所示的茎叶图中,并指出哪个队的身高数据方差较小(无需计算);
(2)现从两队所有身高超过178cm的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() ,其中
,其中 ![]() =(2cosx,﹣
=(2cosx,﹣ ![]() sin2x),
sin2x), ![]() =(cosx,1),x∈R.
=(cosx,1),x∈R.
(1)求f(x)的周期及单调递增区间;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,f(A)=﹣1,a= ![]() ,且向量
,且向量 ![]() 与
与 ![]() 共线,求边长b和c的值.
共线,求边长b和c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+ax+b,g(x)=x2+cx+d,且f(2x+1)=4g(x),f′(x)=g′(x),f(5)=30,求a,b,c,d的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线![]() (
( ![]() 为参数)和定点
为参数)和定点![]() , F1 、 F2 是此圆锥曲线的左、右焦点,以原点 O 为极点,以 x 轴的正半轴为极轴建立极坐标系.
, F1 、 F2 是此圆锥曲线的左、右焦点,以原点 O 为极点,以 x 轴的正半轴为极轴建立极坐标系.
(1)求直线 AF2 的直角坐标方程;
(2)经过点 F1 且与直线AF2 垂直的直线 l 交此圆锥曲线于M,N 两点,求||MF1|-|NF1|| 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com