解:(1)由已知

,
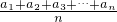
=(2n-1)a
n,分别取n=2,3,4,5,
得
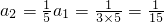
,

,
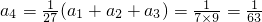
,

;
所以数列的前5项是:

,

,

,

,
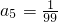
; …(5分)
(2)由(1)中的分析可以猜想
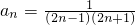
(n∈N
*). …(7分)
下面用数学归纳法证明:
①当n=1时,猜想显然成立. …(8分)
②假设当n=k(k≥1且k∈N
*)时猜想成立,即

. …(9分)
那么由已知,得

,
即a
1+a
2+a
3+…+a
k=(2k
2+3k)a
k+1.所以(2k
2-k)a
k=(2k
2+3k)a
k+1,
即(2k-1)a
k=(2k
2+3)a
k+1,又由归纳假设,得

,
所以

,即当n=k+1时,猜想也成立. …(11分)
综上①和②知,对一切n∈N*,都有
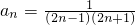
成立. …(12分)
分析:(1)利用数列{a
n}前n项的算术平均数等于第n项的2n-1倍,推出关系式,通过n=2,3,4,5求出此数列的前5项;
(2)通过(1)归纳出数列{a
n}的通项公式,然后用数学归纳法证明.第一步验证n=1成立;第二步,假设n=k猜想成立,然后证明n=k+1时猜想也成立.
点评:本题是中档题,考查数列的项的求法,通项公式的猜想与数学归纳法证明方法的应用,注意证明中必须用上假设,考查计算能力,分析问题解决问题的能力.

 ,且前n项的算术平均数等于第n项的2n-1倍(n∈N*).
,且前n项的算术平均数等于第n项的2n-1倍(n∈N*). ,
,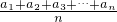 =(2n-1)an,分别取n=2,3,4,5,
=(2n-1)an,分别取n=2,3,4,5,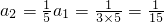 ,
, ,
,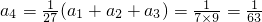 ,
, ;
; ,
, ,
, ,
, ,
,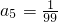 ; …(5分)
; …(5分)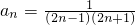 (n∈N*). …(7分)
(n∈N*). …(7分) . …(9分)
. …(9分) ,
, ,
, ,即当n=k+1时,猜想也成立. …(11分)
,即当n=k+1时,猜想也成立. …(11分)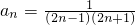 成立. …(12分)
成立. …(12分)
