解:(1)

=t
1
+t
2
=t
1(0,2)+t
2(4,4)=(4t
2,2t
1+4t
2).
当点M在第二或第三象限时,等价于
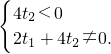
,故所求的充要条件为t
2<0且t
1+2t
2≠0.
(2)证明:当t
1=1时,由(1)知

=(4t
2,4t
2+2).
∵

=

-

=(4,4),

=

-

=(4t
2,4t
2)=t
2(4,4)=t
2
,
∴不论t
2为何实数,A、B、M三点共线.
(3)当t
1=a
2时,

=(4t
2,4t
2+2a
2). 又∵

=(4,4),

⊥

,
∴4t
2×4+(4t
2+2a
2)×4=0,∴t
2=-

a
2,∴

=(-a
2,a
2).又∵|

|=4

,
点M到直线AB:x-y+2=0的距离d=
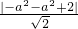
=

|a
2-1|.
∵S
△ABM=12,∴

|

|•d=

×4

×

|a
2-1|=12,解得a=±2,
故所求a的值为±2.
分析:(1)由条件求出点M的坐标,利用点M在第二或第三象限的充要条件为横坐标小于0,纵坐标不等于0,得到结果.
(2)由条件求出

的坐标,证明

等于一个实数与

的乘积,即

∥

,即证明了A、B、M三点共线.
(3)先求出

的坐标,用点到直线的距离公式求出点M到直线AB的距离,由三角形面积等于12解出a的值.
点评:本题考查两个向量坐标形式的运算法则,证明三点共线的方法,向量的模及点到直线的距离公式的应用,体现了转化的数学思想,准确进行坐标运算,是解题的难点和关键.

 =t1
=t1 +t2
+t2 .
. ⊥
⊥ 且△ABM的面积为12时,a的值.
且△ABM的面积为12时,a的值. =t1
=t1 +t2
+t2 =t1(0,2)+t2(4,4)=(4t2,2t1+4t2).
=t1(0,2)+t2(4,4)=(4t2,2t1+4t2).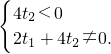 ,故所求的充要条件为t2<0且t1+2t2≠0.
,故所求的充要条件为t2<0且t1+2t2≠0. =(4t2,4t2+2).
=(4t2,4t2+2). =
= -
- =(4,4),
=(4,4), =
= -
- =(4t2,4t2)=t2(4,4)=t2
=(4t2,4t2)=t2(4,4)=t2 ,
, =(4t2,4t2+2a2). 又∵
=(4t2,4t2+2a2). 又∵ =(4,4),
=(4,4), ⊥
⊥ ,
, a2,∴
a2,∴ =(-a2,a2).又∵|
=(-a2,a2).又∵| |=4
|=4 ,
,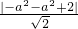 =
= |a2-1|.
|a2-1|. |
| |•d=
|•d= ×4
×4 ×
× |a2-1|=12,解得a=±2,
|a2-1|=12,解得a=±2, 的坐标,证明
的坐标,证明  等于一个实数与
等于一个实数与 的乘积,即
的乘积,即  ∥
∥ ,即证明了A、B、M三点共线.
,即证明了A、B、M三点共线. 的坐标,用点到直线的距离公式求出点M到直线AB的距离,由三角形面积等于12解出a的值.
的坐标,用点到直线的距离公式求出点M到直线AB的距离,由三角形面积等于12解出a的值.
