Question

12．如图，正方体ABCD-A₁B₁C₁D₁的棱长为1，E，F分别是棱DD₁和AB上的点，则下列说法中正确的是②③④（填上所有正确命题的序号）
①A₁C⊥平面B₁EF；
②在平面A₁B₁C₁D₁内总存在与平面B₁EF平行的直线；
③△B₁EF在侧面BCC₁B₁上的正投影是面积为定值的三角形；
④当E，F分别是DD₁和AB的中点时，EF与平面BCC₁B₁所成角的正切值为$\frac{{\sqrt{5}}}{5}$．

Answer 1

分析 利用正方体的特征，对所给的几个命题用线面，面面之间的位置关系，对各项进行依次判断即可．

解答 解：对于①：A₁C⊥平面B₁EF；不一定成立，A₁C垂直平面AC₁D，而平面B₁EF与平面AC₁D不一定平行．故①不对．
对于②：在平面A₁B₁C₁D₁内总存在与平面B₁EF平行的直线；因为这个两个平面是相交的，一个平面平行与两个平面的交线的一定平行与另一个平面，因此该结论正确．故②对．
对于③：△B₁EF在侧面BCC₁B₁上的正投影是面积为定值的三角形．因为其投影是三角形的一边是棱BB₁，E点的投影总落在CC₁到棱BB₁的长度是不变的，故而正投影是三角形面积为定值的．故③对．
对于④：当E，F分别是DD₁和AB的中点时，EF与平面BCC₁B₁所成角的正切值为$\frac{{\sqrt{5}}}{5}$．EF与平面BCC₁B₁所成角等于EF与DAA₁D₁所成角，连接AE，FA⊥DAA₁D₁，则∠FEA为EF与DAA₁D₁所成角．tan∠FEA$\frac{AF}{AE}=\frac{\sqrt{5}}{5}$．故④对．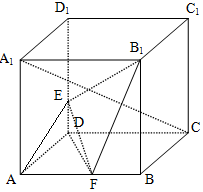

故答案为：②③④．

点评 本题考查了正方体的几何特征，以及线面，面面之间的位置关系，垂直关系的判断，直线与平面所成的角．是一道综合题，属于中档题．