
| A. | [-3,$\frac{1}{2}$] | B. | [-2,2] | C. | [-2,$\frac{1}{2}$] | D. | [-3,-2] |
分析 利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域求出y的值域即可,求解一元二次不等式化简集合B,然后由交集的运算性质计算得答案.
解答 解:A={y|y=sinx-$\sqrt{3}$cosx}={y|y=2sin(x-$\frac{π}{3}$)}=[-2,2],
B={x|2x2+5x-3≤0}={x|$-3≤x≤\frac{1}{2}$}=[-3,$\frac{1}{2}$],
则A∩B=[-2,2]∩[-3,$\frac{1}{2}$]=[-2,$\frac{1}{2}$].
故选:C.
点评 本题考查了交集及其运算,考查了两角和与差的正弦函数公式,以及正弦函数的定义域与值域,考查了一元二次不等式的解法,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(文)试卷(解析版) 题型:选择题
已知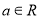 ,“
,“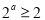 ”是“函数
”是“函数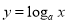 在
在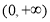 上为减函数”的( )
上为减函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
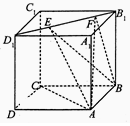 如图,正方体ABCD-A1B1C1D1的棱长为2,线段D1B1上有两个动点E、F,且EF=1,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为2,线段D1B1上有两个动点E、F,且EF=1,则下列结论中错误的是( )| A. | AC⊥BE | B. | AA1∥平面BEF | ||
| C. | 三棱锥A-BEF的体积为定值 | D. | △AEF的面积和△BEF的面积相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 2$\sqrt{7}$ | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com