
| A. | ①② | B. | ①③ | C. | ①④ | D. | ②④ |
分析 在①中,由线面垂直的性质定理得m∥n;在②中,n与α相交、平行或n?α;在③中,m与β相交、平行或m?β,;在④中,由面面垂直的判定定理得α⊥β.
解答 解:由m,n为两条不同的直线,α,β为两个不重合的平面,知:
在①中,若m⊥α,n⊥α,则由线面垂直的性质定理得m∥n,故①正确;
在②中,若m⊥α,n⊥m,则n与α相交、平行或n?α,故②错误;
在③中,若α⊥β,m∥α,则m与β相交、平行或m?β,故③错误;
在④中,若m⊥α,m∥β,则由面面垂直的判定定理得α⊥β,故④正确.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源:2017届江西吉安一中高三上学期段考一数学(理)试卷(解析版) 题型:选择题
已知函数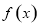 与
与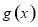 满足:
满足: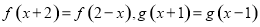 ,且
,且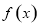 在区间
在区间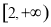 上为减函数,令
上为减函数,令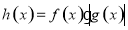 ,则下列不等式正确的是( )
,则下列不等式正确的是( )
A.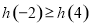 B.
B.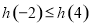 C.
C.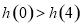 D.
D.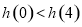
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥P-ABCD中,底面ABCD是棱长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC中点,若H为PD上的动点,EH与平面PAD所成最大角的正切值为$\frac{\sqrt{6}}{2}$.
如图,已知四棱锥P-ABCD中,底面ABCD是棱长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC中点,若H为PD上的动点,EH与平面PAD所成最大角的正切值为$\frac{\sqrt{6}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不超过20的非负实数 | |
| B. | 方程x2-9=0在实数范围内的解 | |
| C. | $\sqrt{3}$的近似值的全体 | |
| D. | 临川十中2016年在校身高超过170厘米的同学的全体 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+2x+5<0 | B. | ?x∈R,x2+2x+5≥0 | C. | ?x∈R,x2+2x+5≥0 | D. | ?x∈R,x2+2x+5≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,$\frac{1}{2}$] | B. | [-2,2] | C. | [-2,$\frac{1}{2}$] | D. | [-3,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com