
| A. | ?x∈R,x2+2x+5<0 | B. | ?x∈R,x2+2x+5≥0 | C. | ?x∈R,x2+2x+5≥0 | D. | ?x∈R,x2+2x+5≤0 |
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:高中数学 来源:2017届江苏南通市如东县等高三10月联考数学试卷(解析版) 题型:解答题
在互联网时代,网校培训已经成为青年学习的一种趋势,假设某网校的套题每日的销售量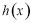 (单位:千套)与销售价格
(单位:千套)与销售价格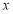 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式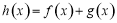 (
(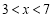 ,
,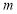 为常数),其中
为常数),其中 与
与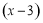 成反比,
成反比,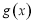 与
与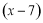 的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套.
的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套.
(1) 求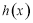 的表达式;
的表达式;
(2) 假设网校的员工工资,办公等所有开销折合为每套题3元(只考虑销售出的套数),试确定销售价格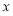 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(文)试卷(解析版) 题型:选择题
已知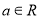 ,“
,“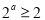 ”是“函数
”是“函数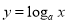 在
在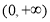 上为减函数”的( )
上为减函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com