
分析 分别根据指数幂的运算性质计算即可.
解答 解:(1)原式=$(\frac{5}{3})^{2×\frac{1}{2}}$+100+$(\frac{4}{3})^{3×(-\frac{2}{3})}$-3+$\frac{37}{48}$=$\frac{5}{3}$+100+$\frac{9}{16}$-3+$\frac{37}{48}$=100.
(2)原式=$(-\frac{3}{2})^{3×(-\frac{2}{3})}$+$50{0}^{\frac{1}{2}}$-$\frac{10}{\sqrt{5}-2}$+1
=$\frac{4}{9}$+10$\sqrt{5}$-10$\sqrt{5}$-20+1=-$\frac{167}{9}$.
点评 本题考查了指数幂的运算性质,属于基础题.


科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(文)试卷(解析版) 题型:选择题
一个几何体的三视图如图所示(图中小方格均为边长为1的正方形),该几何体的体积是( )
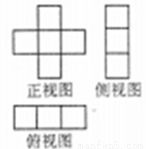
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+2x+5<0 | B. | ?x∈R,x2+2x+5≥0 | C. | ?x∈R,x2+2x+5≥0 | D. | ?x∈R,x2+2x+5≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com