
分析 (I)利用f(x+1)•f(x)=x2+x,对一切x恒成立,得到k;
(II)由( I)得到k为1,即f(x)的解析式,代入h(x),判断函数在[m,m+1]的单调性,得到关于m的方程组解之.
解答 解:(I)f(x+1)•f(x)=k(x+1)•kx=k2(x2+x)
所以(k2-1)(x2+x)=0对一切x恒成立,k2-1=0,得k=±1;
故f(x)=±x; …6分
(II)因f(x)为R上的增函数,
所以f(x)=x,则$h(x)=\frac{x+1}{x-1}=1+\frac{1}{x-1},x≠1$
而h(x)在(-∞,1)和(1,-∞)上是减函数,
于是h(x)在[m,m+1]上单调递减,…8分
则$\left\{\begin{array}{l}h(m)=m+1\\ h(m+1)=m\end{array}\right.$解得m=-1或m=2. …12分.
点评 本题考查了函数解析式的求法以及函数单调性的运用;属于中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | $\sqrt{10}$ | C. | $\sqrt{14}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
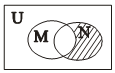 设全集U={1,2,3,4,5,6,7},集合M={1,2,3,5},N={2,4,5},则Venn图中阴影部分表示的集合是( )
设全集U={1,2,3,4,5,6,7},集合M={1,2,3,5},N={2,4,5},则Venn图中阴影部分表示的集合是( )| A. | {1,3} | B. | {4} | C. | {3,5} | D. | {5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16dm2 | B. | 18 dm2 | C. | $18\sqrt{3}$dm2 | D. | $16\sqrt{3}$dm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com