
分析 (1)根据直线l的方程可得直线经过定点H(1,1),而点H到圆心C(0,1)的距离为1,小于半径,故点H在圆的内部,故直线l与圆C相交,命题得证.
(2)把线段的长度比转化为两个向量的关系,由向量的坐标运算得到A,B两点横坐标间的关系,联立直线与圆的方程化为关于x的一元二次方程,由根与系数关系得到A,B两点横坐标的和,求出其中一点的横坐标,最后再代入关于x的方程得到关于m的方程,求解得到m的值,则直线方程可求.
解答 解:(1)由于直线l的方程是mx-y+1-m=0,即 y-1=m(x-1),经过定点H(1,1),
而点H到圆心C(0,1)的距离为1,小于半径$\sqrt{5}$,故点H在圆的内部,故直线l与圆C相交,
故直线和圆恒有两个交点.;
(2)设A(x1,y1),B(x2,y2),由$\frac{AP}{PB}$=$\frac{1}{2}$,得$\overrightarrow{AP}$=$\frac{1}{2}$$\overrightarrow{PB}$,
∴1-x1=$\frac{1}{2}$(x2-1),化简的x2=3-2x1…①
又由直线代入圆的方程,消去y得:(1+m2)x2-2m2x+m2-5=0…(*)
∴x1+x2=$\frac{2{m}^{2}}{1+{m}^{2}}$…②
由①②解得x1=$\frac{3+{m}^{2}}{1+{m}^{2}}$代入(*)式解得m=±1,
∴直线l的方程为x-y=0或x+y-2=0
点评 本题考查了与直线有关的动点的轨迹方程,考查了直线与圆的关系,体现了数学转化思想方法,考查了学生的灵活处理问题的能力和计算能力,是中高档题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(文)试卷(解析版) 题型:选择题
已知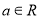 ,“
,“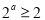 ”是“函数
”是“函数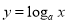 在
在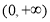 上为减函数”的( )
上为减函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
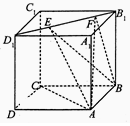 如图,正方体ABCD-A1B1C1D1的棱长为2,线段D1B1上有两个动点E、F,且EF=1,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为2,线段D1B1上有两个动点E、F,且EF=1,则下列结论中错误的是( )| A. | AC⊥BE | B. | AA1∥平面BEF | ||
| C. | 三棱锥A-BEF的体积为定值 | D. | △AEF的面积和△BEF的面积相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,7] | B. | [2,7] | C. | [-2,14] | D. | [2,14] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 2$\sqrt{7}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com