
 如图,已知四棱锥P-ABCD中,底面ABCD是棱长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC中点,若H为PD上的动点,EH与平面PAD所成最大角的正切值为$\frac{\sqrt{6}}{2}$.
如图,已知四棱锥P-ABCD中,底面ABCD是棱长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC中点,若H为PD上的动点,EH与平面PAD所成最大角的正切值为$\frac{\sqrt{6}}{2}$.分析 (1)首先要证明AE⊥平面PAD,则∠EHA为EH与平面PAD所成的角;所以当AH最短时,∠EHA最大;即当AH⊥PD时,∠EHA最大;接着利用构造平行四边形法判定线面平行即可;
(2)利用已知条件证明平面PAB⊥平面ABCD,PB⊥面CQM,所求二面角转化到Rt△CQM中即可;
解答 (1)证明:连接AC,由题设知△ABC为正三角形,所以AE⊥BC,
又BC∥AD,因此AE⊥AD;
∵PA⊥平面ABCD,AE?平面ABCD,
∴PA⊥AE
而PA?平面PAD,AD?平面PAD,且PA∩AD=A,
所以AE⊥平面PAD,
则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE=$\sqrt{3}$
所以当AH最短时,∠EHA最大;
即当AH⊥PD时,∠EHA最大;
此时tan∠EHA=$\frac{AE}{AH}$=$\frac{\sqrt{3}}{AH}$=$\frac{\sqrt{6}}{2}$,
因此AH=$\sqrt{2}$,
又AD=2,∴∠ADH={45°}∴PA=2
∴H为PD的中点,
取PA的中点M,连接HM,MB,则HM=$\frac{1}{2}AD\$且HM∥AD,DB=$\frac{1}{2}$AD且DB∥AD,
∴HM∥DB且HM=DB
∴四边形DHMB为平行四边形
∴EH∥BM,
又BM?平面PAB
∴EH∥平面PAB.
(2)解: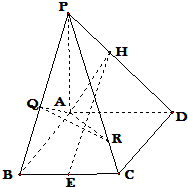 ∵PA⊥面ABCD,PA?平面PAB,
∵PA⊥面ABCD,PA?平面PAB,
∴平面PAB⊥平面ABCD,
∵PB?面PAB∴CM⊥PB,
∴PB⊥面CQM,∴$PB⊥MC\\∴∠CQM为二面角A-PB-A的平面角\\∵AB=BC=2,∠ABC={60^0}$,
∴△ABC为正三角形,∴点M为AB的中点,
∴$CM=\sqrt{3}\\ 在等腰直角△PAB中,由等面积可算出QM=\frac{{\sqrt{2}}}{2},\\∵Q{C^2}=Q{M^2}+C{M^2}$,∴$QC=\frac{{\sqrt{14}}}{2}$,
∴$在Rt△CQM中有:cos∠CQM=\frac{QM}{QC}=\frac{{\frac{{\sqrt{2}}}{2}}}{{\frac{{\sqrt{14}}}{2}}}=\frac{{\sqrt{7}}}{7}\\ 二面角A-PB-A的余弦值为\frac{{\sqrt{7}}}{7}\end{array}$.
点评 本题主要考查了构造平行四边形法判定直线与平面平行,以及空间二面角的求法知识点,属中等题.


科目:高中数学 来源:2017届江西吉安一中高三上学期段考一数学(理)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
如图所示,已知 为
为 的
的 边上一点,
边上一点, 经过点
经过点 ,交
,交 于另一点
于另一点 ,
, 经过点
经过点 ,交
,交 于另一点
于另一点 与
与 交于点
交于点 .
.

(1)求证: ;
;
(2)若 的半径为5,圆心
的半径为5,圆心 到直线
到直线 的距离为3,
的距离为3, 切
切 于点
于点 ,求线段
,求线段 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
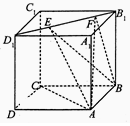 如图,正方体ABCD-A1B1C1D1的棱长为2,线段D1B1上有两个动点E、F,且EF=1,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为2,线段D1B1上有两个动点E、F,且EF=1,则下列结论中错误的是( )| A. | AC⊥BE | B. | AA1∥平面BEF | ||
| C. | 三棱锥A-BEF的体积为定值 | D. | △AEF的面积和△BEF的面积相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com