在等差数列{an}中.首项a1=0.公差d≠0.若ak=a1+a2+-+a17.则k=137．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

15．在等差数列{a_n}中，首项a₁=0，公差d≠0，若a_k=a₁+a₂+…+a₁₇，则k=137．

分析由a_k=a₁+a₂+…+a₁₇=$\frac{17（{a}_{1}+{a}_{17}）}{2}$=17a₉，再利用通项公式即可得出．

解答解：∵a_k=a₁+a₂+…+a₁₇=$\frac{17（{a}_{1}+{a}_{17}）}{2}$=17a₉，
∴0+（k-1）d=17（0+8d），
∴k=136+1=137．
故答案为：137．

点评本题考查了等差数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：2017届江西吉安一中高三上学期段考一数学（理）试卷（解析版） 题型：解答题

在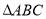中，角的对边分别为，，且．

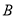（1）求角的大小；

（2）若等差数列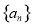的公差不为零，且，且成等比数列，求的前项和．

查看答案和解析>>

科目：高中数学 来源：2017届湖南永州市高三高考一模考试数学（文）试卷（解析版） 题型：解答题

已知曲线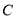上的任一点到点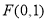的距离减去它到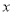轴的距离的差都是1.

（1）求曲线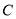的方程；

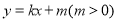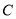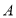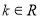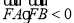（2）设直线与曲线交于，两点，若对于任意都有，求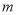的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

3．若f（x）=$\left\{\begin{array}{l}{f（x-5），x＞0}\\{{2}^{x+2}{+∫}_{0}^{\frac{π}{6}}cos3tdt，x≤0}\end{array}\right.$，则f（2017）=（　　）

A．

$\frac{1}{3}$

B．

$\frac{1}{6}$

C．

$\frac{5}{6}$

D．

$\frac{1}{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

10．

如图，已知四棱锥P-ABCD中，底面ABCD是棱长为2的菱形，PA⊥平面ABCD，∠ABC=60°，E是BC中点，若H为PD上的动点，EH与平面PAD所成最大角的正切值为$\frac{\sqrt{6}}{2}$．
（1）当EH与平面PAD所成角的正切值为$\frac{\sqrt{6}}{2}$时，求证：EH∥平面PAB；（2）在（1）的条件下，求二面角A-PB-C的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

20．已知函数f（x）=x²-x+ce^-2x（c∈R）．
（1）若f（x）是在定义域内的增函数，求c的取值范围；
（2）若函数F（x）=f（x）+f'（x）-$\frac{5}{2}$（其中f'（x）为f（x）的导函数）存在三个零点，求c的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

7．下列各组对象不能构成一个集合的是（　　）

	A．	不超过20的非负实数
	B．	方程x²-9=0在实数范围内的解
	C．	$\sqrt{3}$的近似值的全体
	D．	临川十中2016年在校身高超过170厘米的同学的全体

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

3．定义在R上的函数f（x）满足（x-1）f′（x）≤0，且f（-x）=f（2+x），当|x₁-1|＜|x₂-1|时，有（　　）

A．

f（2-x₁）≥f（2-x₂）

B．

f（2-x₁）=f（2-x₂）

C．

f（2-x₁）＞f（2-x₂）

D．

f（2-x₁）≤f（2-x₂）

查看答案和解析>>