
����Ŀ��ij��ѧҪ�Ӹ�һ�꼶�ס��������༶��ѡ��һ����μ��е���̨��֯�ġ�����֪ʶ������.��У�Լס�������IJ���ѡ�֣�ÿ��7�ˣ�������һ�λ���֪ʶ���ԣ�����ȡ�õijɼ�������100�֣��ľ�Ҷͼ��ͼ��ʾ�����мװ�ѧ����ƽ������85�֣��Ұ�ѧ���ɼ�����λ����85.

��1����![]() ��ֵ��
��ֵ��
��2�����ݾ�Ҷͼ����ס�������ͬѧ�ɼ��ķ���Ĵ�С������ͳ��ѧ�Ƕȷ�������УӦѡ��װ���Ұ����.
���𰸡���1��![]() ��
��![]() ��2��Ӧ��ѡ���Ұ����
��2��Ӧ��ѡ���Ұ����
��������
��1����֪�װ�ѧ����ƽ������85������ƽ������ʽ���������![]() ����֪�Ұ�ѧ���ɼ�����λ����85��������λ���Ķ���������
����֪�Ұ�ѧ���ɼ�����λ����85��������λ���Ķ���������![]() ��ֵ��
��ֵ��
��2����֪�װ�ѧ����ƽ������85�����ݷ���Ĺ�ʽ����������װ�ͬѧ�ɼ��ķ�����ݾ�Ҷͼ�����Լ�����Ұ�ͬѧ��ƽ���֣��ٸ��ݷ���Ĺ�ʽ������Ұ�ͬѧ�ɼ��ķ���Ƚ����������С���ó�����.
�⣺��1����Ϊ�װ�ѧ����ƽ������85��
����![]() ��
��
���![]() .
.
��Ϊ�Ұ�ѧ���ɼ�����λ����85������![]() .
.
��2���ɣ�1����֪��![]() ��
��
����![]()
![]() .
.
�ɾ�Ҷͼ�ɵã�![]() ��
��
����![]()
![]() ��
��
����![]() .
.
�ʸ�УӦ��ѡ���Ұ����.


 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳������н���������˿���һ��������Ʒ�ɲμ�һ�γ齱.���ų齱�����Ч��չ������齱�������Խ��Խ�࣬���̳���ǰ5��齱�����������ͳ�ƣ�y��ʾ��x��μӳ齱����������õ�ͳ�Ʊ����£�
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
������һ��ͳ�Ʒ���������y��x����������ع�ϵ.
��1��������5�������ȡ���죬��������1��μӳ齱��������70�ĸ��ʣ�
��2��������ϱ��ṩ�����ݣ�����С���˷����y����x�����Իع鷽��![]() �������Ƹû����7�죬���ж������˿Ͳμӳ齱��
�������Ƹû����7�죬���ж������˿Ͳμӳ齱��
�ο���ʽ�����ݣ�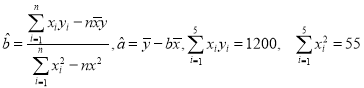 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=alnx+ ![]() x2��ax��aΪ��������������ֵ�㣮
x2��ax��aΪ��������������ֵ�㣮
��1����ʵ��a��ȡֵ��Χ��
��2����f��x����������ֵ��ֱ�Ϊx1 �� x2 �� ������ʽf��x1��+f��x2�����ˣ�x1+x2�����������˵���Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}��ǰn���ΪSn �� ������S4=24��S7=63�� ����������{an}��ͨ�ʽ��
������ ![]() ��������{bn}��ǰn���Tn ��
��������{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1������![]() �����ֵ��
�����ֵ��
��2������������![]() ������
������![]() ������ʵ��
������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���Ƿ����ʵ��![]() ��ʹ�ò���ʽ
��ʹ�ò���ʽ![]() ��������
��������![]() ������������ڣ����
������������ڣ����![]() ��ȡֵ��Χ���������ڣ�˵������.
��ȡֵ��Χ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ʵ��a��b��c��d���� ![]() =1������e����Ȼ�����ĵ�������a��c��2+��b��d��2����СֵΪ�� ��
=1������e����Ȼ�����ĵ�������a��c��2+��b��d��2����СֵΪ�� ��
A.4
B.8
C.12
D.18
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C���Եı߷ֱ�Ϊa��b��c����֪ ![]() ��sinA=
��sinA= ![]() �� ������sinC��ֵ��
�� ������sinC��ֵ��
��II����DΪAC���е㣬����ABC�����Ϊ8 ![]() ����BD�ij���
����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=sin2x+2sinxcosx+3cos2x�� ��������f��x���ĵ����������䣻
������x��[0�� ![]() ]������f��x������ֵ����Ӧx��ȡֵ��
]������f��x������ֵ����Ӧx��ȡֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����![]() ��ǰ
��ǰ![]() ���У�������ĺ�Ϊ56��ż����ĺ�Ϊ48����
���У�������ĺ�Ϊ56��ż����ĺ�Ϊ48����![]() ������
������![]() ��.
��.
��1��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ��
��![]() ,����
,����![]() ������һ���ȱ����У�����
������һ���ȱ����У�����![]() ��
��![]() ��������
��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��3��������ʵ��![]() ��
��![]() ��ʹ��
��ʹ��![]() ������
������![]() ���������
���������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com