
 ×3×4×3+
×3×4×3+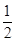 ×3×4×4=102(cm3).--------------8分
×3×4×4=102(cm3).--------------8分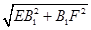 =
=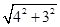
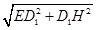 =
=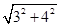


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源:不详 题型:解答题
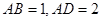 ,
,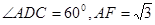 .
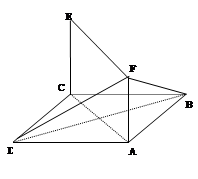
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
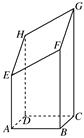
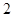 的正方形
的正方形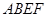 中,
中,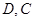 分别为
分别为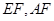 上的点,且
上的点,且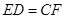 ,现沿
,现沿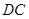 把
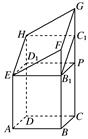
把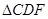 剪切、拼接成如图(2)的图形,再将
剪切、拼接成如图(2)的图形,再将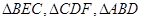 沿
沿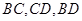 折起,使
折起,使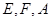 三点重合于点
三点重合于点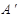 。
。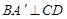 ;
;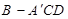 体积的最大值。
体积的最大值。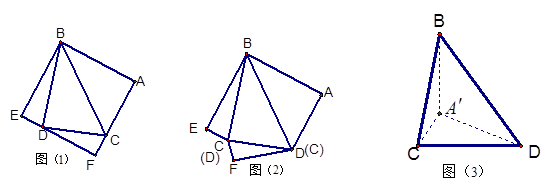
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 内的两条直线垂直,则
内的两条直线垂直,则 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com