|
|
|
若复数i·(1+ai)是纯虚数,则实数a的值是
|
| [ ] |
A. |
1
|
B. |
-1
|
C. |
0
|
D. |
0或-1
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且AF⊥PE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知向量a=(sinx,-1),b=(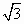 cosx,- cosx,-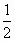 ),函数f(x)=(a+b)·a-2. ),函数f(x)=(a+b)·a-2.
(Ⅰ)求函数f(x)的最小正周期T;
(Ⅱ)已知a、b、c分别为△ABC内角A、B、C的对边,其中A为锐角,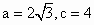 且f(A)=1,求A,b和△ABC的面积S. 且f(A)=1,求A,b和△ABC的面积S.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设P是△ABC内任意一点,S△ABC表示△ABC的面积,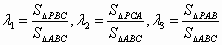 ,定义f(P)=(λ1,λ2,λ3),若G是△ABC的重心, ,定义f(P)=(λ1,λ2,λ3),若G是△ABC的重心, ,则 ,则
|
| [ ] |
A. |
点Q在△GAB内
|
B. |
点Q在△GBC
|
C. |
点Q在△GCA
|
D. |
点Q与点G重合
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,在正三棱柱ABC-DEF中,AB=2,AD=1.P是CF的延长线上一点,FP=t.过A,B,P三点的平面交FD于M,交FE于N.
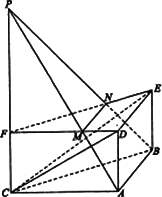
(Ⅰ)求证:MN∥平面CDE;
(Ⅱ)当平面PAB⊥平面CDE时,求t的值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
某几何体的三视图如下图所示,则该几何体的表面积为
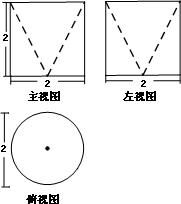
|
| [ ] |
A. |
(5+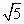 )π )π
|
B. |
(20+2 )π )π
|
C. |
(10+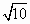 )π )π
|
D. |
(5+2 )π )π
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知函数f(x)=asinx+bx3+5,且f(1)=3,则f(-1)=________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知直线l:Ax+By+C=0(A,B不全为0),两点P1(x1,y1),P2(x2,y2),若(Ax1+By1+C)·(Ax2+By2+C)>0,|Ax1+By1+C|>|Ax2+By2+c|,则
|
| [ ] |
A. |
直线l与直线P1P2不相交
|
B. |
直线l与线段P2P1的延长线相交
|
C. |
直线l与线段P1P2的延长线相交
|
D. |
直线l与线段P1P2相交
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
某产品的广告费用x与销售额y的统计数据如下表

根据上表可得回归方程 = = x+ x+ 中的 中的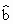 为9.4,据此模型预报广告费用为6万元时销售额为 为9.4,据此模型预报广告费用为6万元时销售额为
|
| [ ] |
A. |
63.6万元
|
B. |
65.5万元
|
C. |
67.7万元
|
D. |
72.0万元
|
|
|
查看答案和解析>>
