（12分）定义在区间(－1，1)上的函数f (x)满足：①对任意的x，y∈(－1，1)，都有f (x)
+ f (y) =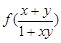
; ②当x∈(－1，0)，f (x) > 0.
（1）求证f (x)为奇函数；
（2）试解不等式：f (x) + f (x－1) 
.
（1）略
（2）不等式的解集为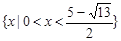
【解析】解：（1）解：令x = y = 0，则
f (0) + f
(0) = 
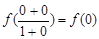∴ f (0) = 0
令x∈(－1, 1) ∴－x∈(－1, 1)
∴ f (x) + f (－x) = f (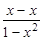
) = f (0) = 0
∴ f (－x) =－f (x)
∴ f (x) 在(－1，1)上为奇函数…………………4分
（2）解：令－1< x1 < x2 < 1
则f (x1) －f (x2) = f (x1) + f
(－x2) =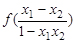 
∵x1－x2 < 0，1－x1x2 > 0
∴
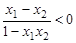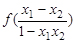∴ > 0
∴ f (x1) > f (x2) ∴ f (x) 在(－1，1)上为减函数
又f (x) + f (x－1) >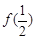
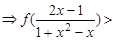
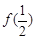…………………8分
∴ 不等式化为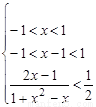
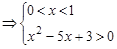
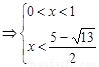或
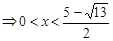
∴ 不等式的解集为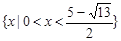…………………12分
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案科目：高中数学 来源： 题型：
| f(a)+f(b) | a+b |
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
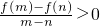
）+f（x-1）＜0，求x的取值范围查看答案和解析>>
科目：高中数学 来源： 题型：
（ⅰ）f（－1）=f（1）=0;
（ⅱ）对任意的u，v∈［－1，1］，都有|f（u）－f（v）|≤|u－v|.
（Ⅰ）证明：对任意的x∈［－1，1］，都有x－1≤f（x）≤1－x;
（Ⅱ）证明：对任意的u,v∈［－1，1］,都有|f（u）－f（v）|≤1；
（Ⅲ）在区间［－1，1］上是否存在满足题设条件的函数y=f（x），且使得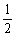
若存在，请举一例；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
（ⅰ）f（－1）=f（1）=0；
（ⅱ）对任意的u，v∈［－1，1］，都有|f（u）－f（v）|≤|u－v|.
（Ⅰ）证明：对任意的x∈［－1，1］，都有x－1≤f（x）≤1－x；
（Ⅱ）判断函数g（x）=
，是否满足题设条件；
（Ⅲ）在区间［－1，1］上是否存在满足题设条件的函数y=f（x），且使得对任意的u，v∈［－1，1］，都有|f（u）－f（v）|=|u－v|.
若存在，请举一例；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年安徽省安庆市望江中学高三（上）第一次月考数学试卷（理科）（解析版） 题型：解答题
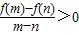
）+f（x-1）＜0，求x的取值范围查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com