练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列命题正确的个数是：（ ）

    ①对于两个分类变量与的随机变量的观测值来说，越小，判断“与有关系”的把握程度越大；

    ②在相关关系中，若用拟合时的相关指数为，用拟合时的相关指数为，且，则的拟合效果好；

    ③利用计算机产生之间的均匀随机数，则事件“”发生的概率为；

    ④“”是“”的充分不必要条件

    A. B. C. D.

    【答案】C

    【解析】分析：根据独立性检验的性质可判断①；根据回归分析的基本原理可判断②；根据几何概型概率公式可判断③； 根据不等式的性质可判断④.

    详解：①对于两个分类变量与的随机变量的观测值来说，越小，判断“与有关系”的把握程度越小，①错误；

    ②在相关关系中，若用拟合时的相关指数为，用拟合时的相关指数为，且，则的拟合效果好，②正确；

    ③利用计算机产生之间的均匀随机数，则事件“”发生的概率为，正确；

    ④“”可得到“”， “”时“”不一定成立，所以“”是“”的充分不必要条件，正确，即正确命题的个数是，故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知定义在R上的函数f（x）＝｜x﹣m｜+｜x｜，m∈N*，存在实数x使f（x）＜2成立．

    （1）求实数m的值；

    （2）若α≥1，β≥1，f（α）+f（β）＝4，求证：≥3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

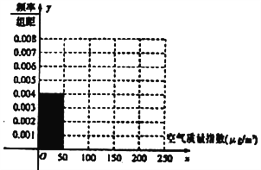
    【题目】全世界越来越关注环境保护问题，某监测站点于2018年1月某日起连续天监测空气质量指数()，数据统计如下：

    空气质量指数()

    空气质量等级

    空气优

    空气良

    轻度污染

    中度污染

    重度污染

    天数

    20

    40

    10

    5

    （1）根据所给统计表和频率分布直方图中的信息求出，的值，并完成频率分布直方图；

    （2）由频率分布直方图，求该组数据的众数和中位数；

    （3）在空气质量指数分别属于和的监测数据中，用分层抽样的方法抽取天，再从中任意选取天，求事件“两天空气都为良”发生的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是某小区2017年1月至2018年1月当月在售二手房均价（单位：万元/平方米）的散点图.（图中月份代码1—13分别对应2017年1月—2018年1月）

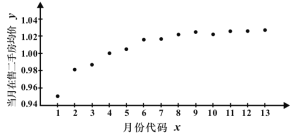
    由散点图选择和两个模型进行拟合，经过数据处理得到两个回归方程分别为和，并得到以下一些统计量的值：

    残差平方和

    0.000591

    0.000164

    总偏差平方和

    0.006050

    （1）请利用相关指数判断哪个模型的拟合效果更好；

    （2）某位购房者拟于2018年6月份购买这个小区平方米的二手房（欲

    购房为其家庭首套房）.若购房时该小区所有住房的房产证均已满2年但未满5年，请你利用（1）中拟合效果更好的模型估算该购房者应支付的购房金额.（购房金额=房款+税费；房屋均价精确到0.001万元/平方米）

    附注：根据有关规定，二手房交易需要缴纳若干项税费，税费是按房屋的计税价格进行征收.（计税价格=房款），征收方式见下表：

    契税

    （买方缴纳）

    首套面积90平方米以内（含90平方米）为1%；首套面积90平方米以上且144平方米以内（含144平方米）为1.5%；面积144平方米以上或非首套为3%

    增值税

    （卖方缴纳）

    房产证未满2年或满2年且面积在144平方米以上（不含144平方米）为5.6%；其他情况免征

    个人所得税

    （卖方缴纳）

    首套面积144平方米以内（含144平方米）为1%；面积144平方米以上或非首套均为1.5%；房产证满5年且是家庭唯一住房的免征

    参考数据：，，，，，，，. 参考公式：相关指数.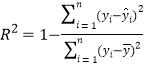

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝alnx﹣ex（a∈R）．其中e是自然对数的底数．

    （1）讨论函数f（x）的单调性并求极值；

    （2）令函数g（x）＝f（x）+ex，若x∈[1，+∞）时，g（x）≥0，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的一个焦点与上、下顶点构成直角三角形，以椭圆的长轴长为直径的圆与直线相切.

    （1）求椭圆的标准方程；

    （2）设过椭圆右焦点且不平行于轴的动直线与椭圆相交于两点，探究在轴上是否存在定点，使得为定值？若存在，试求出定值和点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（12分）

    炼钢是一个氧化降碳的过程，由于钢水含碳量的多少直接影响冶炼时间的长短，因此必须掌握钢水含碳量和冶炼时间的关系.现已测得炉料熔化完毕时钢水的含碳量x与冶炼时间y（从炉料熔化完毕到出钢的时间）的一组数据，如下表所示：

    （1）据统计表明，之间具有线性相关关系，请用相关系数r加以说明（ ，则认为y与x有较强的线性相关关系，否则认为没有较强的线性相关关系，r精确到0.001）；

    （2）建立y关于x的回归方程（回归系数的结果精确到0.01）；

    （3）根据（2）中的结论，预测钢水含碳量为160个0.01%的冶炼时间.

    参考公式：回归方程中斜率和截距的最小二乘估计分别为，

    ，相关系数

    参考数据：，

    .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）求函数的单调区间；

    （Ⅱ）若函数上是减函数，求实数a的最小值；

    （Ⅲ）若，使（）成立，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为纪念重庆黑山谷晋升国家5A级景区五周年，特发行黑山谷纪念邮票，从2017年11月1日起开始上市．通过市场调查，得到该纪念邮票在一周内每1张的市场价y（单位：元）与上市时间x（单位：天）的数据如下：

    上市时间x天

    1

    2

    6

    市场价y元

    5

    2

    10

    （Ⅰ）分析上表数据，说明黑山谷纪念邮票的市场价y（单位：元）与上市时间x（单位：天）的变化关系，并判断y与x满足下列哪种函数关系，①一次函数；②二次函数；③对数函数，并求出函数的解析式；

    （Ⅱ）利用你选取的函数，求黑山谷纪念邮票市场价最低时的上市天数及最低的价格．

    查看答案和解析>>

    同步练习册答案