

分析 (1)利用线面平行的性质判断并证明直线DC与直线m的位置关系;
(2)A1D在平面A1OB中的射影为A1O,OG⊥A1O,即可求出A1G的长;
(3)求出O到平面A1DB的距离,即可求直线A1O与平面A1BD所成角的正弦值.
解答  解:(1)∵DC∥OB,DC?平面A1OB,OB?平面A1OB
解:(1)∵DC∥OB,DC?平面A1OB,OB?平面A1OB
∴DC∥平面A1OB,
∵m为平面A1DC与平面A1OB的交线,
∴DC∥m;
(2)由题意,A1D在平面A1OB中的射影为A1O,
∴OG⊥A1O,∴A1G=2A1O=4;
(3)△A1OB中,A1B=$\sqrt{4+4-2×2×2×(-\frac{1}{2})}$=2$\sqrt{3}$,
∵A1D=DB=2$\sqrt{2}$,∴${S}_{△{A}_{1}DB}$=$\frac{1}{2}×2\sqrt{3}×\sqrt{8-3}$=$\sqrt{15}$,
设O到平面A1DB的距离为h,则$\frac{1}{3}\sqrt{15}•h=\frac{1}{3}•\frac{1}{2}•2•2•\frac{\sqrt{3}}{2}$,
∴h=$\frac{\sqrt{5}}{5}$,
∵A1O=2,
∴直线A1O与平面A1BD所成角的正弦值=$\frac{\sqrt{5}}{10}$.
点评 本题考查线面平行的判定与性质,考查线面垂直的证明,考查线面角,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
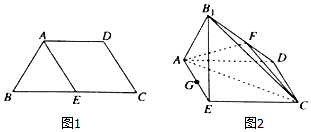 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使平面B1AE⊥平面ABCD,F,G分别为B1D,AE的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使平面B1AE⊥平面ABCD,F,G分别为B1D,AE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=2-$\frac{1}{{2}^{n}}$ | B. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$<1 | ||
| C. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=1 | D. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\sqrt{2})$ | B. | $(-∞,-\frac{{\sqrt{2}}}{2})$ | C. | $(-\sqrt{2},\frac{{\sqrt{2}}}{2})$ | D. | $(-∞,\sqrt{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数$f(x)=2sin(2x+φ)\;(|φ|<\frac{π}{2})$部分图象如图所示.
已知函数$f(x)=2sin(2x+φ)\;(|φ|<\frac{π}{2})$部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 12cm2 | B. | 15πcm2 | C. | 24πcm2 | D. | 36πcm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com