
分析 作出区域D对应的图象,则区域D关于原点对称,若函数等分区域,则等价满足函数为奇函数即可.
解答 解:作出区域D对应的图象,则区域D关于原点对称,
若函数等分区域D,
则函数应该是原因原点对称的奇函数,
①y=sinx•cosx=$\frac{1}{2}$sin2x是奇函数,满足等分区域D,
②y=x3+$\frac{1}{2016}$x,是奇函数,满足等分区域D,
③y=ex-1为非奇非偶函数,不能平分,
④y=|x|-$\frac{3}{4}$是偶函数,不能平分,
⑤y=-$\frac{9}{2}{x^2}+\frac{5}{8}$是偶函数,不能平分.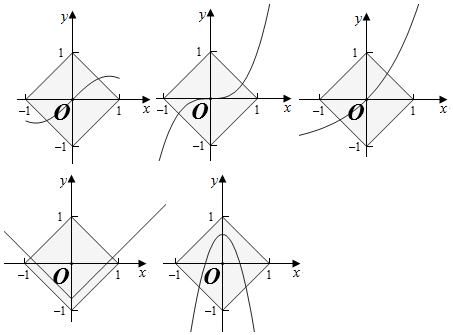
故答案为:①②.
点评 本题主要考查与函数图象有关的命题的真假判断,根据新定义转化为判断函数的奇偶性是解决本题的关键.综合性较强,有一定的难度.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图(1),在等腰梯形ABCD中,AB∥CD,E,F分别为AB和CD的中点,且AB=EF=2,CD=4,M为CE中点,现将梯形ABCD沿EF所在直线折起,使平面EFCB⊥平面EFDA,如图(2)所示,N是CD的中点.
如图(1),在等腰梯形ABCD中,AB∥CD,E,F分别为AB和CD的中点,且AB=EF=2,CD=4,M为CE中点,现将梯形ABCD沿EF所在直线折起,使平面EFCB⊥平面EFDA,如图(2)所示,N是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
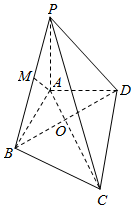 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A${\;}_{100}^{14}$ | B. | A${\;}_{100}^{15}$ | C. | A${\;}_{100}^{16}$ | D. | A${\;}_{100}^{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com