解:(1)f′(x)=

-

=

设h(x)=x
2-(2a+1)x+a
2,其判别式△=4a+1,
①当a≤-

时,△≤0,f′(x)≥0,f(x)在定义域(0,+∞)上是增函数;
当△>0时,由h(x)=x
2-(2a+1)x+a
2=0解得:x
1=

,x
2=
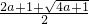
(每个根1分)
②当-

<a<0时,△>0,2a+1>0;此时,x
2>x
1>0,即h(x)在定义域(0,+∞)上有两个零点x
1=

,x
2=
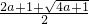
在区间(0,x
1)上,h(x)>0,f′(x)>0,f(x)为(0,x
1)上的增函数
在区间(x
1,x
2)上,h(x)<0,f′(x)<0,f(x)为(x
1,x
2)上的增函数
在区间(x
2,+∞)上,h(x)>0,f′(x)>0,f(x)为(x
2,+∞)上的增函数.
③当a=0时,x
1=0,x
2=1,在区间(0,1)上,h(x)<0,f′(x)<0;在区间(1,+∞)上,h(x)>0,f′(x)>0,…(7分)
④当a>0时,函数f(X)的定义域是(0,a)∪(a,+∞),
∵h(a)=-a<0,h(x)在(0,a)上有零点x
1,在(a,+∞)上有零点x
2;
在区间(0,x
1)和(x
2,+∞)上,f′(x)>0,f(x)在(0,x
1)和(x
2,+∞)上为增函数;
在区间(x
1,a)和(a,x
2)上,f′(x)<0,f(x)在(x
1,a)和(a,x
2)上为减函数.
综上:当a≤-

时,函数f(x)的递增区间是(0,+∞);当-

<a<0时,f(x)的递增区间是(0,x
1)和(x
2,+∞),递减区间是(x
1,x
2);当a=0时,f(x)的递减区间是(0,1);递增区间是(1,+∞);当a>0时,f(x)的递减区间(x
1,a)和(a,x
2),递增区间是(0,x
1)和(x
2,+∞).
(2)当a≤0时,g(x)的定义域是(0,+∞);当a>0时,f(x)的定义域是(0,a)∪(a,+∞),
g′(x)=

,令t(x)=x(1-lnx),则t′(x)=-lnx(每个导数1分)
在区间(0,1)上,t′(x)=-lnx>0,t(x)=x(1-lnx)是增函数且0<t(x)<1;
在区间(1,+∞)上,t′(x)=-lnx<0,t(x)=x(1-lnx)是减函数且t(x)<1;
当x=1时,t(1)=1.
故当a≥1时,g′(x)≤0,g(x)无极大值;
当0<a<1时,t(a)-a≠0,方程t(x)=a在区间(0,1)和(1,+∞)上分别有一解x′,x″,
此时函数g(x)在x=x″处取得极大值;
当a≤0时,方程t(x)=a在区间[e,+∞)上有一解x•,此时函数g(x)在x=x•处取得极大值.
综上所述,若g(x)有极大值,则a的取值范围是(-∞,1).
分析:(1)对函数f(x)求导,当导数f'(x)大于0时可求单调增区间,当导数f'(x)小于0时可求单调减区间.
(2)先对a分情况求出g(x)的定义域,再在区间(0,1)和区间(1,+∞)上研究函数的单调性,进而研究极值的存在性,即可求出a的范围.
点评:本题主要考查通过求函数的导数来确定函数增减区间的问题,考查利用导数研究函数的极值问题,有一定的综合性.

 ,g(x)=
,g(x)=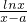 ,a是常数.
,a是常数. -
- =
=
 时,△≤0,f′(x)≥0,f(x)在定义域(0,+∞)上是增函数;
时,△≤0,f′(x)≥0,f(x)在定义域(0,+∞)上是增函数; ,x2=
,x2=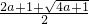 (每个根1分)
(每个根1分) <a<0时,△>0,2a+1>0;此时,x2>x1>0,即h(x)在定义域(0,+∞)上有两个零点x1=
<a<0时,△>0,2a+1>0;此时,x2>x1>0,即h(x)在定义域(0,+∞)上有两个零点x1= ,x2=
,x2=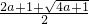
 时,函数f(x)的递增区间是(0,+∞);当-
时,函数f(x)的递增区间是(0,+∞);当- <a<0时,f(x)的递增区间是(0,x1)和(x2,+∞),递减区间是(x1,x2);当a=0时,f(x)的递减区间是(0,1);递增区间是(1,+∞);当a>0时,f(x)的递减区间(x1,a)和(a,x2),递增区间是(0,x1)和(x2,+∞).
<a<0时,f(x)的递增区间是(0,x1)和(x2,+∞),递减区间是(x1,x2);当a=0时,f(x)的递减区间是(0,1);递增区间是(1,+∞);当a>0时,f(x)的递减区间(x1,a)和(a,x2),递增区间是(0,x1)和(x2,+∞). ,令t(x)=x(1-lnx),则t′(x)=-lnx(每个导数1分)
,令t(x)=x(1-lnx),则t′(x)=-lnx(每个导数1分)

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案