
【题目】【选修4-4:坐标系与参数方程】
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的极坐标方程和
的极坐标方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与曲线
与曲线![]() 分别交于第一象限内的
分别交于第一象限内的![]() ,
,![]() 两点,求
两点,求![]() .
.
科目:高中数学 来源: 题型:
【题目】某公司有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出![]() 名员工从事第三产业,调整后他们平均每人每年创造利润为
名员工从事第三产业,调整后他们平均每人每年创造利润为![]() 万元(
万元(![]() ),剩下的员工平均每人每年创造的利润可以提高
),剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则调整员工从事第三产业的人数应在什么范围?
(2)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的两个焦点分别为F1,F2,离心率为
(a>b>0)的两个焦点分别为F1,F2,离心率为![]() ,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
(1)求椭圆C的方程;
(2)若直线y=kx+b与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据调查显示,某高校![]() 万男生的身高服从正态分布
万男生的身高服从正态分布![]() ,现从该校男生中随机抽取
,现从该校男生中随机抽取![]() 名进行身高测量,将测量结果分成
名进行身高测量,将测量结果分成![]() 组:
组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并绘制成如图所示的频率分布直方图.
,并绘制成如图所示的频率分布直方图.
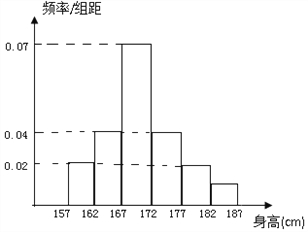
(Ⅰ)求这![]() 名男生中身高在
名男生中身高在![]() (含
(含![]() )以上的人数;
)以上的人数;
(Ⅱ)从这![]() 名男生中身高在
名男生中身高在![]() 以上(含
以上(含![]() )的人中任意抽取
)的人中任意抽取![]() 人,该
人,该![]() 人中身高排名(从高到低)在全校前
人中身高排名(从高到低)在全校前![]() 名的人数记为
名的人数记为![]() ,求
,求![]() 的数学期望.
的数学期望.
(附:参考数据:若![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“每天锻炼一小时,健康工作五十年,幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关,从单位随机抽取30名员工进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
爱好 | 10 | ||
不爱好 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到爱好运动的员工的概率是![]() .
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料分析能否有把握认为爱好运动与性别有关?
(2)若从这30人中的女性员工中随机抽取2人参加一活动,记爱好运动的人数为![]() ,求
,求![]() 的分布列、数学期望.参考数据:
的分布列、数学期望.参考数据:
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划销售某种食品,现邀请甲、乙两个商家进场试销10天.两个商家提供的返利方案如下:甲商家每天固定返利60元,且每卖出一件食品商家再返利3元;乙商家无固定返利,卖出30件以内(含30件)的食品,每件食品商家返利5元,超出30件的部分每件返利8元.经统计,两个商家的试销情况茎叶图如下:
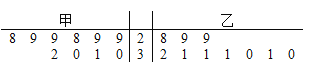
(1)现从甲商家试销的10天中抽取两天,求这两天的销售量都小于30的概率;
(2)若将频率视作概率,回答以下问题:
① 记商家乙的日返利额为X(单位:元),求X的分布列和数学期望;
② 超市拟在甲、乙两个商家中选择一家长期销售,如果仅从日平均返利额的角度考虑,请利用所学的统计学知识为超市作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①函数![]() 为奇函数;②当
为奇函数;②当![]() 时,
时,![]() ;③
;③![]() 是函数
是函数![]() 的一个零点这三个条件中任选一个,补充在下面问题中,并解答,已知函数
的一个零点这三个条件中任选一个,补充在下面问题中,并解答,已知函数![]() ,
,![]() 的图象相邻两条对称轴间的距离为
的图象相邻两条对称轴间的距离为![]() ,______.
,______.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 在
在![]() 上的单调递增区间.
上的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
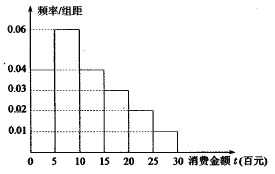
【题目】“双十一”已经成为网民们的网购狂欢节,某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查,用随机抽样的方法抽取了100人,其消费金额![]() (百元)的频率分布直方图如图所示:
(百元)的频率分布直方图如图所示:
(1)求网民消费金额![]() 的平均值和中位数
的平均值和中位数![]() ;
;
(2)把下表中空格里的数填上,能否有![]() 的把握认为网购消费与性别有关;
的把握认为网购消费与性别有关;
男 | 女 | 合计 | |
| |||
| 30 | ||
合计 | 45 |
附表:
|
|
|
|
|
|
|
|
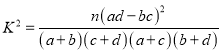 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com